다중회귀분석을 해볼까요.
다중회귀분석을 위해 사용할 변수는
더미 변수를 포함해서
여학생더미, 학업열의, 학업 무기력을 독립변수로 하고
자아존중감을 종속변수로 해보겠습니다.
1. 더미변수 만들기
더미변수를 만들기 위해서는 범주형 변수, 명목형 변수에서
관심있는 변수를 제외하고 모드 0으로 코딩하여, 변수 간의 차이를 확인할 수 있습니다.
여학생더미는 남학생을 0으로, 여학생을 1로 코딩하면 되겠습니다.
변수 변환을 위해
변환 탭 - 다른 변수로 코딩 변경을 눌러줍니다.

그리고 성별 변수를 클릭 해서 화살표를 눌러줍니다.
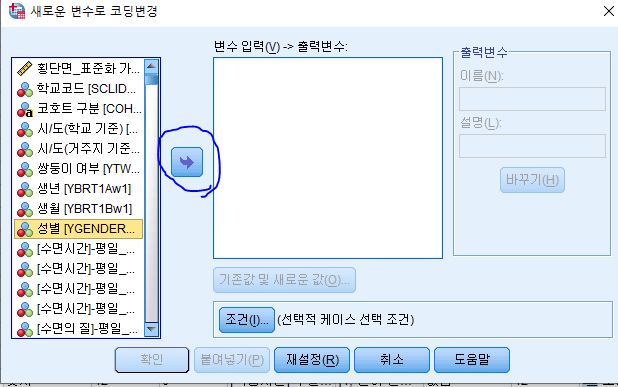
출력변수의 이름 칸에 이름을 지정해주시고 바꾸기를 누릅니다.
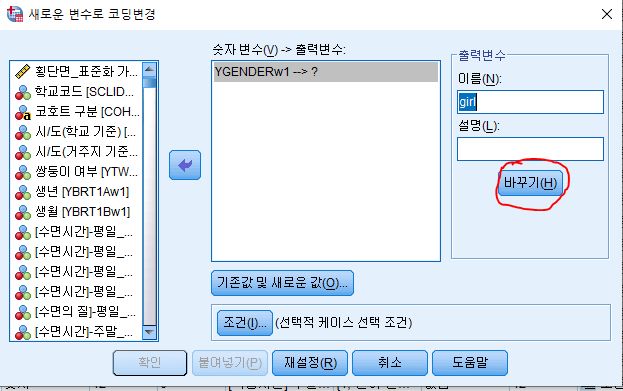
그런 다음 기존 값 및 새로운 값을 눌러줍니다.

원래 데이터에서는 남자는 1 여자는 2로 코딩되어 있습니다.
여기서 기존값의 '값'에는 원래 값,
새로운 값의 '기준값'에는 바꾸고자 하는 값을 넣습니다.
남자는 1에서 0으로, 여자는 2에서 1로 바꿔줍니다.
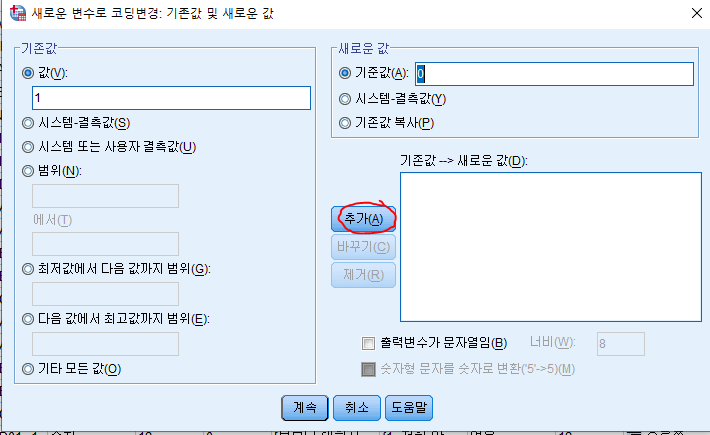
각각 1과 0을 넣고 추가를 넣어줍니다.
그리고 2와 1을 넣어주면 되겠죠
다 추가한 다음, 계속을 눌러줍니다.
그러면 다시 이 화면이 나오는데
여기서 다시 '확인'을 눌러줍니다. 그러면 끝입니다.
2. 다중회귀분석
회귀분석과 마찬가지로,
분석탭에서 회귀분석 - 선형을 눌러줍니다.
그러면 종속변수에 자아존중감을 넣어주고
독립변수에 여학생 더미, 학업열의, 학업 무기력을 넣어줍니다.
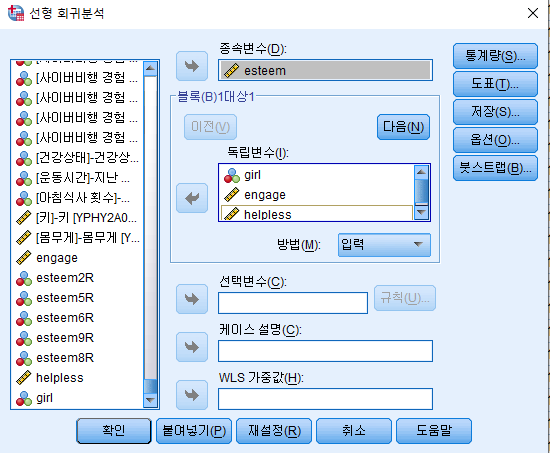
그리고 '통계량'을 눌러주어서
공선성 진단을 체크해줍니다. 그리고 계속을 누르고 확인을 눌러주면..
분석결과가 사악 나오네요.
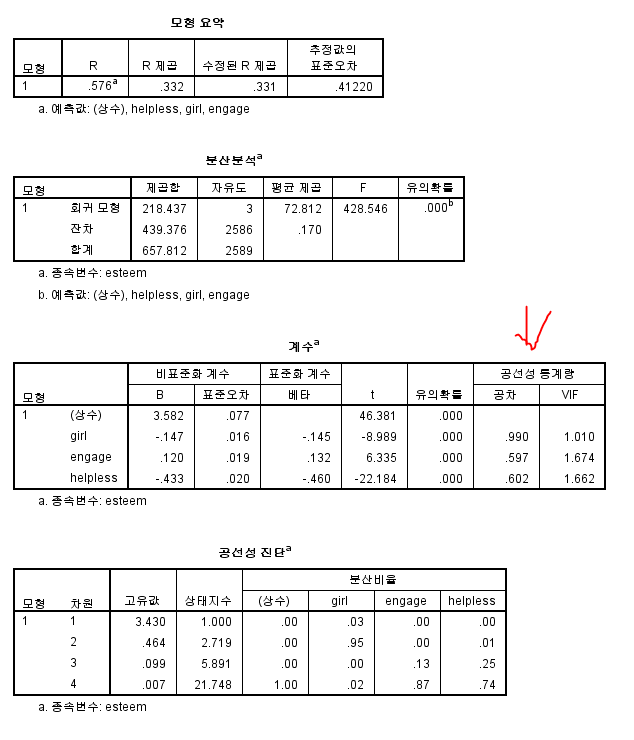
모형 요약을 보시면,

R제곱값이 .332가 나오네요,
이는 여학생더미, 학업열의, 학업 무기력이 자아존중감의 약 33.2%를 설명하고 있는 것으로 나옵니다.
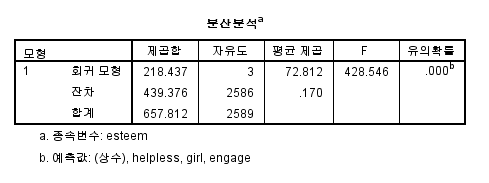
분산분석에서는, 회귀모형 자체에 대한 검정으로 F검정을 실시하는데
유의확률 .000 으로 문제없어 보이네요.
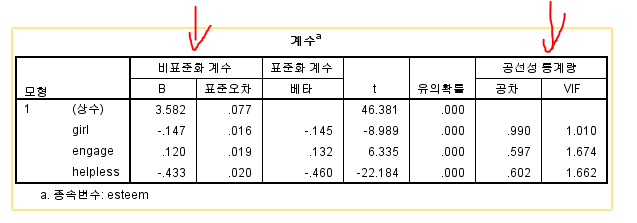
'공선성 통계량'을 보시면, 변수들 간의 다중 공선성을 확인해줍니다.
다양한 변수를 투입하게되면, 독립변수들 간에 상관이 높게 나타날 경우가 존재할 수 있습니다.
이럴경우에, 결과값이 왜곡될 수 있어 체크를 해주어야 합니다.
공차값이 0.1 보다 작거나, VIF값이 10보다 크게 되면 다중공선성이 있음을 고려해보아야 합니다.
다행히(?) 지금 분석 결과는 0.1보다 크고, VIF값이 10보다 작아 괜찮아 보입니다.ㅋㅋ
마지막으로 계수값을 보면,
상수항, 여학생더미, 학업열의, 학업 무기력의 계수 값을 확인할 수 있네요.
모든 변수가 유의확률 .000으로 유의수준 .001에서 모두 통계적으로 유의한 것으로 나옵니다.
먼저 비표준화계수로 식을 작성해보면,
자아존중감 = 3.582 + (-.147*여학생더미)+.120*학업열의 +(-.433*학업무기력) + e
더미 변수를 먼저 해석하자면, 남학생의 자아존중감은 3.582 정도 되는데, 여학생의 자아존중감은
이보다 -.147점 낮은 것으로 나타났습니다.
학업열의는 1단위 높아질 수록 .120만큼 자아존중감이 높아지고,
학업무기력은 1단위 낮아질 수록, -.433만큼 자아존중감이 낮아지는 것으로 나옵니다.
다음, 표준화계수로 변수 간의 상대적 영향력을 살펴보면
학업무기력이 -.460으로 가장 크고, 그다음은 여학생더미(-.145), 학업열의(.132) 순으로
자아존중감에 영향을 주는 것으로 나타났습니다.(절대값 기준인거는 아시죠..?ㅋㅎ)
이렇게 해석을 스윽해보고 표로 정리해보면,
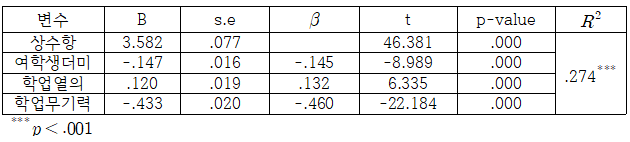
다중회귀분석에서 이 정도면 뭐 괜찮지 않나 싶네요..ㅋㅋ
'교육통계 > spss' 카테고리의 다른 글
| 교육통계 SPSS - 6. 매개효과분석 (0) | 2022.11.04 |
|---|---|
| 교육통계 SPSS - 5. 위계적회귀분석 (0) | 2022.11.04 |
| 교육통계 SPSS - 3. 회귀분석 (0) | 2022.11.04 |
| 교육통계 SPSS - 2. 상관분석 (0) | 2022.11.04 |
| 교육통계 SPSS - 1. 변수생성&기술통계 (0) | 2022.11.04 |