안녕하세요. 이번에는 저번에 이어 더미변수를 포함한 다중회귀분석과 위계적회귀분석에 대해 알아보겠습니다.
-------------------------------------------------------------------------------------------------------------------------------
1. 더미변수
더미변수는 범주형 변수를 분석에 사용하기 위해 코딩을 해주는 것을 뜻합니다.
예를 들어, 남자 1 여자 2로 조사를 받았는데,
이전의 연속변수들 처럼 이 둘을 합쳐서 성별변수를 만든다고하면...
평균이 뭐 1.2, 1.3 이런식으로 나올텐데
소숫점으로 나오는 결과는 해석이 불가능 하겠죠?ㅎㅎ
따라서 기준이 되는 변수를 0으로 하고 그 외 변수는 1로 만들어서
해석을 좀 더 용이하게 하기 위한 과정이라 할 수 있습니다.
만약, 남자를 0으로, 여자를 1로 코딩하여 더미변수를 투입해서 결과를 보면
0일때와 1일때로 분류해서 해석을 좀 더 편하게 할 수 있습니다.
성별외의 더미변수로 지역변수를 사용하기도 하죠.
지역변수를 대도시, 중소도시, 읍면지역 이런식으로 나누어진다고 하면 범주가 3개가 있네요
그럼 기준을 읍면지역으로 한다면,
중소도시더미: 읍면지역 0, 중소도시 1, 대도시 0
대도시더미: 읍면지역 0, 중소도시 0, 대도시 1
이렇게 2개를 만들어서 사용해야 합니다.
범주갯수 -1 만큼 더미변수를 만들어서 투입해야 합니다.
그럼 이제 실습을 위해 변수를 만들어 보겠습니다.
성별조사문항을 통해서 여학생더미를 만들어 보겠습니다(남학생 : 0, 여학생 : 1)
계속 사용하던 KCYP2018 패널자료를 사용합니다.

[그림 1] 성별조사문항 확인
남학생은 1, 여학생은 2로 조사가 되었습니다.
문항코딩은 YGENDERw2 이구요.
남학생은 0, 여학생을 1로 만들려면 모든 행에서 1을 빼면 됩니다.

[그림 2] 더미코딩
study 데이터셋에 girl이라는 열을 만들고, YGENDERw2가 17열이니까, study[,17]로 17번째 열을 고정한 다음, -1해서 17번째 열의 모든 행에서 1씩 빼줍니다.
그러면 계산이 완료 되었네요.
참 쉽죠?
-------------------------------------------------------------------------------------------------------------------------------
2. 더미변수를 포함한 다중회귀분석
그럼 이제 더미변수를 투입해서 다중회귀분석을 해보겠습니다.
먼저, 학업열의, 자아존중감, 학업무기력, 여학생더미 변수를 데이터프레임으로 만들겠습니다.

[그림 4] 변수 4개를 데이터프레임으로 묶죠
기술통계, 상관은 여기서 설명 안 드려도 되겠죠..?ㅎ
바로 다중회귀로 넘어가겠습니다ㅎㅎ
마찬가지로 자아존중감을 종속변수, 나머지 변수들은 모두 독립변수입니다.

[그림 5] 다중회귀분석 코드
lmresult3 <- lm(formula = study.esteem ~ study.engage + study.helpless + study.girl, data = sample3)
이렇게 study.girl 변수만 새롭게 추가되었습니다.
summary를 통해 결과를 확인하면 [그림 6]과 같습니다.
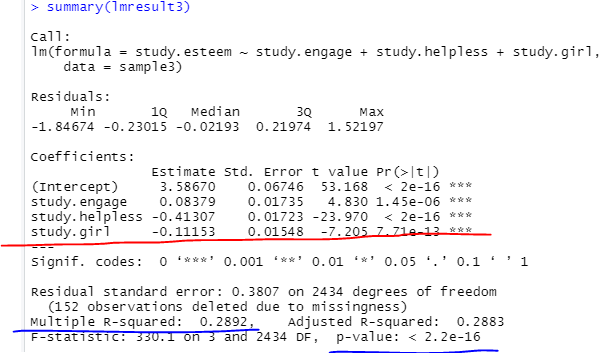
해석방법은 더미변수만 다루도록 하겠습니다.
저번장에서 신나게 했으니까요..ㅎㅎ
해석에서 봐주어야 할 것은 상수항과 여학생더미의 비표준화회귀계수 값 입니다.
일단 상수항은 3.586이고, 여학생더미는 -0.11153 이면서 유의수준 0.001에서 통계적으로 유의하네요.
회귀식을 작성해보면
자아존중감 = -0.1115*여학생더미 + 0.0837*학업열의 -0.4130*학업무기력 + 3.586 + e 가 되겠죠?
여기서 상수항의 의미는 중학교 2학년 남학생의 자아존중감이 됩니다.
왜냐면, 상수항만 본다는 것은 모든 변수들 값이 0일때를 의미하는 것이죠?
그러면 모두 0이라는 것은 여학생더미도 0, 즉 남학생을 의미하는 것입니다.
그리고 여학생더미가 1이 되면, 여학생을 의미하는 것입니다.
아까 0은 남학생, 1은 여학생으로 코딩했으니까요!
따라서,
여학생은 남학생에 비해 자아존중감이 -0.1115 점 낮은 것으로 나타나며, 유의수준 0.001에서 통계적으로 유의하였다.
라고 해석이 가능해지는 것입니다.
마무리로 표준화 회귀계수도 추가해서 다시 한 번 표로 정리해보겠습니다.
표준화회귀계수는 QuantPsyc 패키지의 lm.beta함수를 활용합니다.

[그림 7] 표준화 회귀계수
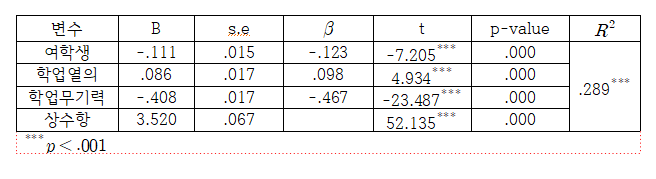
이렇게 더미변수까지 포함한 다중회귀분석을 해보았습니다. ㅎ
-------------------------------------------------------------------------------------------------------------------------------
3. 위계적회귀분석
위계적 회귀분석은 위계적(hierarchical)이라는 용어를 보면 알 수 있듯이
투입되는 독립변수들 사이에 위계적 관계가 있으면서,
독립변수들이 분석에 투입되는 순서에 따라 회귀모형의 설명력이 얼마만큼 커지는 지, 설명력의 변화가 통계적으로
유의한지에 대해 목적을 두는 분석방법 이라 할 수 있습니다.
회귀분석을 연습하면서 R-square 값을 확인할 수 있습니다.
이는 종속변수의 분산을 독립변수들이 얼마나 설명할 수 있는지를 알려주는 수치인데요, 그래서 설명력이라는 말을
쓰는 것 같기도 합니다.
위계적 회귀분석에서 중요한 것은 독립변수들의 위계적 관계를 설정하는 것이죠.
이 역시 탄탄한 이론적 배경을 가지고 있어야 교수님께 혼나지 않습니다!
여기선.. 음. .. 귀찮아요 ㅎ
그럼 바로 분석연습으로 들어가 볼까요?
-------------------------------------------------------------------------------------------------------------------------------
독립변수들의 투입 순서를 위해 '모형'으로 그 위계를 표현합니다.
모형1, 모형2, 모형3으로 점점 커지면서 독립변수를 점차 추가하는 것이죠.
여기서도 종속변수는 자아존중감을, 독립변수는 여학생더미, 학업열의, 학업무기력 이렇게만 사용하겠습니닿
그러면 모형 설정은
모형1: 여학생더미
모형2: 여학생더미, 학업열의
모형3: 여학생더미, 학업열의, 학업무기력
이렇게 됩니다.
앞서 회귀분석할 때 lmresult라는 객체에 값을 담았는데,
직관적으로 알기 쉽게 model1, model2, model3으로 각 분석을 해보겠습니다.

[그림 8] 위계적 회귀분석 준비
첫번째는 여학생더미만
두 번째는 여학생더미에 학업열의
세 번째는 여학생더미에 학업열의에 학업무기력까지 추가한 것을 확인할 수 있죠?ㅎ
그럼 이제 이 회귀모형 간에 설명력 변화가 통계적으로 유의하게 변화하는지 확인하겠습니다.
사용할 함수는 anova입니다.
anova는 F-검증을 하는 함수인데요, 회귀분석을 할 때 F-검증을 통해 회귀모형의 유의도 검사를 하였습니다.
그래서 anova를 사용하는 거죠ㅎㅎ
anova(모형1, 모형2)

[그림 9] 모형비교 함수
결과를 확인해 볼까요?

[그림 10] 모형1-모형2 비교
오 유의수준 0.001에서 통계적으로 유의하게 나왔네요
그럼 모형2와 모형3도 비교해볼까요?

[그림 11] 모형 2-모형3 비교
오 마찬가지로 유의미하게 나오네요.
그럼 이제 결과값들을 쭉 정리를 해주어야 합니다.
summary(model1)
summary(model2)
summary(model3)
으로 나오는 결과를 말이죠...ㅎ
이것을 보고하는 양식 또한 잘 정리하는게 중요하겠죠!
저는 이렇게 합니다ㅎㅎ

다중회귀분석과 다르게 추가된 것은 F값과 R-square 변화량인데요
이에 대한 해석을 꼭 붙여주어야 합니다.
모형1를 분석한 결과 유의수준 0.001에서 통계적으로 유의하였으며(F(2,590) = 29.93), 설명력은 1%였다
모형2를 분석한 결과 유의수준 0.001에서 통계적으로 유의하였으며(F(2,590) = 168.2), 설명력은 12%였고, 모형 1에 비해 모형 2의 설명력은 11% 증가하였다.
모형3을 분석한 결과 유의수준 0.001에서 통계적으로 유의하였으며(F(2,590) = 442.07), 설명력은 28%로 나타났다. 모형2에 비해 모형3의 설명력은 16% 증가하였다.
이렇게 회귀모형에 대한 해석을 한 다음
최종모형인 모형3이 통계적으로 유의했기 때문에, 모형3에서 각 독립변수들에대한 해석을 하면 됩니다.
여학생이 어쩌고, 학업열의가 저쩌구 ..ㅎㅎ
-------------------------------------------------------------------------------------------------------------------------------
이렇게 해서 다중회귀분석과 위계적회귀분석까지 살펴보았는데요,
한편, 단계적 회귀분석(stepwise)방법이라는 것도 있습니다.
이 분석방법은 독립변수를 투입하는 순서를 설명력이 증가하는 크기 순서대로 컴퓨터가 알아서 계산해서 설정하는 방법입니다.
보다시피 설명력은 변수를 투입하면 투입할수록 무조건 더 커집니다. (당연히 통계적으로 유의할 때만)
근데 그냥 막 투입하는 것을 교육학에서는 안 좋아해서...
다른 분야는 잘 모르겠지만, 교육학에서는 잘 안 쓰더라구요..ㅎㅎ
왜냐면 이론적 배경이 무진장 중요하니까요..ㅎㅎㅎ
개념없이 투입했다고 혼나요ㅠㅠ
아무튼 이쯤 회귀분석은 정리하고
다음은 매개분석, 조절효과분석에 대해서 알아보겠습니다.
감사합니다!
'교육통계 > Rstudio' 카테고리의 다른 글
| 교육통계 R랑가몰라 4. 조절효과 1) 범주형변수 (0) | 2022.11.02 |
|---|---|
| 교육통계 R랑가몰라 3. 매개효과분석 (0) | 2022.11.02 |
| 교육통계 R랑가몰라 2. 기초통계 - 2) 회귀분석 (0) | 2022.11.02 |
| 교육통계 R랑가몰라 2. 기초통계 - 1) 상관관계 (0) | 2022.11.02 |
| 교육통계 R랑가몰라 - 1. 기술통계 4) 기술통계 결과확인하기 (0) | 2022.11.02 |