안녕하세요. 이번에는 회귀분석에 대해 알아보겠습니다.
회귀분석은 독립변인의 값을 이용해서 종속 변인의 값을 예측하는 방법입니다.
회귀분석을 위해선 먼저 두 변인간의 관계가 어떤지 상관관계 분석에서 출발합니다.
두 변수간의 상관관계가 통계적으로 유의하다면, 독립변수가 종속 변인에 미치는 영향 역시 생각해볼 수 있겠죠.
회귀분석까지 하는 김에 기술통계부터 산포도 및 상관관계 그리고 회귀분석까지 확인해보겠습니다.
-------------------------------------------------------------------------------------------------------------------------------
1. 기술통계
이번에는 계속 사용하던 학업열의와 자아존중감 변수에 학업무기력 변수를 더해서 분석을 해보겠습니다.
먼저 학업 무기력 변수를 만들고, sample2라는 객체에 학업열의, 자아존중감, 학업무기력 3개의 변수를 데이터 프레임으로 만들겠습니다.
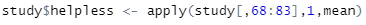
[그림 1] 학업 무기력 변수 생성
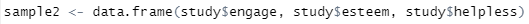
[그림 2] 데이터 프레임 만들기
기술통계에서 사용한 함수는 psych 패키지의 describe 함수를 사용하겠습니다.
[그림 3] 기술통계 코드

[그림 4] 기술통계 결과
이제 이거를 예쁘게(?) 표로 옮겨야겠죠?
<표 1> 기술통계 분석 결과
|
변수
|
사례수
|
평균
|
표준편차
|
최소값
|
최대값
|
왜도
|
첨도
|
|
학업열의
|
2438
|
2.46
|
.51
|
1.00
|
4.00
|
-.11
|
.44
|
|
자아존중감
|
2438
|
2.93
|
.45
|
1.00
|
4.00
|
.11
|
.02
|
|
학업무기력
|
2438
|
1.97
|
.52
|
1.00
|
4.00
|
.07
|
-.27
|
일반적으로 기술통계 분석 결과를 보고할 때 사례수, 평균, 표준편차, 최솟값,왜도, 첨도를 포함합니다.
왜도, 첨도를 보고하는 이유는 자료의 정규분포 검증을 위한 보고입니다.
각각 절댓값이 2,7 이 넘지 않으면 정규분포인 것으로 간주합니다.
출처: Curran, P. J., West, S. G., & Finch, J. F. (1996). The robustness of test statistics to nonnormality and specification error in confirmatory factor analysis. Psychological methods, 1(1), 16.
근데 또 이게 분야마다 더 정규성 검정 기준을 깐깐하게 설정할 수는 있습니다.
표는 음.. 더 예쁘게 만들거나 아님 선행연구에서 보고하는 양식에 맞게 잘 변형하면 될 듯합니다.
저는 미적 감각이 떨어져서...ㅎ
소수점은 보통 둘째 자리까지 보고합니다!
-------------------------------------------------------------------------------------------------------------------------------
2. 산포도 및 상관관계
이제 변수들의 산포도를 확인해볼까요?

[그림 5] 산포도 코드

[그림 6] 산포도 결과
학업열의와 자아존중감은 +방향의 관계를 보이고,
학업 무기력은 -방향을 보이네요.
이어서 상관관계도 확인하겠습니다.
이번엔 바로 psych 패키지 내장 함수인corr.test로 결과와 유의도 값을 보겠습니다.

[그림 7] 상관관계 검정 코드

[그림 8] 상관관계 검정 결과
세 개의 변수간 상관관계가 모두 통계적으로 유의하네요!
아 그래도.. 역시 각각의 유의도 검정을 통해 정확하게 확인해야겠죠..? cor.test함수를 사용합니다.

[그림 9] 상관관계 변수간 상관관계 검정
이렇게 검정을 하면, 순서대로
학업열의 와 자아존중감
학업열의와 학업 무기력
학업 무기력과 자아존중감
을 검정할 수 있습니다.

[그림 10] 학업열의 와 자아존중감 상관관계 검정
상관계수는 0.331 , 유의 수준 0.001에서 통계적으로 유의하네요
[그림 11] 학업열의와 학업 무기력 상관관계 검정
상관계수는 -0.497, 유의 수준 0.001에서 통계적으로 유의하네요
[그림 12] 학업 무기력과 자아존중감 상관관계 검정
상관계수는 -0.516, 유의 수준 0.001에서 통계적으로 유의하네요
보통 논문이나 보고서에 보고할 때 [그림 8], [그림 9], [그림 10]을 다음 <표 1>과 같이 보고합니다.
<표 1> 상관계수 표기
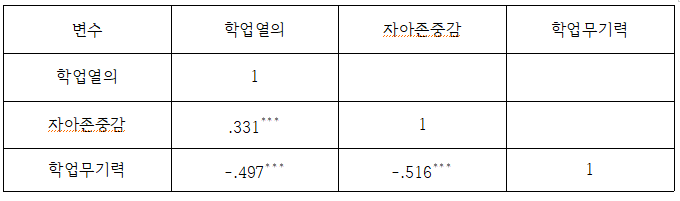
역시, 표 양식은 자신의 미적 역량에 맞게 잘 꾸미면 될 듯합니다 ㅎㅎㅎ
상관계수가 모두 통계적으로 유의하네요!
회귀분석에 변수를 모두 무리 없이 사용할 수 있겠네요.
-------------------------------------------------------------------------------------------------------------------------------
3. 회귀분석
회귀분석을 위해서는 독립변수, 종속변수가 필요합니다.
일단, 단일 회귀분석은 독립변수 1개로 종속변수 1개를 예측하는 분석방법입니다.
이때 독립변수니, 종속변수니 설정은 연구자 마음대로 하기보단
철저한 이론적 고찰에 의거해서 이루어져야 합니다(적어도 사회과학분야에서는요)
안 그러면, 분석 막 했다고 교수님들이 뭐라 하더라고요... 근거 없이 통계만 돌렸다고 ㅋㅋㅋ
하지만 여기선 굳이..ㅎㅎ
임의로 독립변수는 학업열의로 종속변수는 자아존중감으로 하겠습니다.
회귀분석에 사용하는 함수는 lm함수입니다.
lm(formula = 종속변수 ~ 독립변수, data = 데이터셋)
주의하실 점은 독립변수가 뒤에 온다는 것!

종속변수는 study.esteem (변수 이름 정확하게 적어야 합니다!)
독립변수는 study.engage
lmresult라는 객체에 lm함수를 사용해서 회귀분석 결과를 집어넣었습니다.
이렇게 담고 난 다음 summary함수를 사용해서 결과를 확인할 것입니다.
summary(lmresult)로 실행을 하면 [그림 11]을 얻습니다.

[그림 11] 회귀분석 결과
먼저 빨간색 박스를 보면
Coefficients
(Intercept) : 상수항
Estimate : 비표준화 회귀계수
등을 확인할 수 있습니다.
친절하게도 플래그(*)도 붙여서 유의도 검증도 해주네요 ㅎ
이를 토대로 회귀식을 만든다면
자아존중감 = 0.29134*학업열의 + 2.21256(상수항) + e
해석을 하자면 학업열의가 1 단위 올라갈 때, 자아존중감이 0.29134점 더 높아지는 것으로 해석할 수 있으며,
회귀계수는 유의 수준 0.001에서 통계적으로 유의하는 것으로 나왔습니다.
그다음 파란색 박스를 보면
회귀모형에 대한 결괏값을 보고합니다.
R-squared : 설명력, 독립변인이 종속 변인을 설명하는 정도
F-statistic, p-value : F검정 결괏값,회귀모형의 유의도 검증
이 역시 해석을 해보면 학업열의가 자아존중감을 10%(0.1096) 정도 설명하는 것으로 나타나며, 회귀모형이 유의 수준 0.001에서 통계적으로 유의한 것으로 나타났습니다.
-------------------------------------------------------------------------------------------------------------------------------
이번 내용을 정리하자면, 실제 연구에서 사용하는 절차에 따라 회귀분석을 진행해보았습니다.
다음에는 다중회귀를 다루면서 마찬가지로 어떤 식으로 논문에 보고하는지 조금 더 자세하게 다루어보겠습니다.
감사합니다!
'교육통계 > Rstudio' 카테고리의 다른 글
| 교육통계 R랑가몰라 3. 매개효과분석 (0) | 2022.11.02 |
|---|---|
| 교육통계 R랑가몰라 2. 기초통계 - 4) 다중회귀분석2 (0) | 2022.11.02 |
| 교육통계 R랑가몰라 2. 기초통계 - 1) 상관관계 (0) | 2022.11.02 |
| 교육통계 R랑가몰라 - 1. 기술통계 4) 기술통계 결과확인하기 (0) | 2022.11.02 |
| 교육통계 R랑가몰라 - 1. 기술통계 3) 역문항 포함된 변수 만들기 (0) | 2022.11.02 |