안녕하세요. 이번에는 연속형변수를 활용한 조절효과분석에 대해 알아보겠습니다.
분석을 위한 변수로 우울, 사회적 위축, 학업 무기력을 사용하였습니다.
독립변수: 우울
종속변수: 사회적 위축
조절변수: 학업 무기력
-------------------------------------------------------------------------------------------------------------------------------
1. 조절 효과 분석
변수 만드는 과정은 [그림 1]과 같고요 ㅎㅎ

[그림 1] 변수 생성
분석은 앞선 범주형 변수와 같습니다.
lm함수를 사용해서, 상호작용 항을 투입하면 되는 것이지요.

[그림 2] 조절 효과 분석 코드
아 분석 전에 조절 효과를 해석하는데 조금 더 유용하기 위해서 평균중심화평균 중심화를 진행하기도 합니다.
제가 사용한 변수를 이용해서 설명드리면
학업 무기력이 평균인집단과평균 이상 인 집단, 평균 이하인 집단 간의 차이를 좀 더 설명하기 쉽게 됩니다.
그냥 변수를 사용하여 해석하면 어느 기준점을 잡기가 조금 곤란해질 수도 있으니까요
중심화 작업을 하려면 각 변수마다 평균값을 빼주면 중심화(센터링)가 됩니다.
먼저 기술 통계치를 확인해보고

[그림 3] 변수 기술통계
각 변수의 평균값들을 빼서 평균이 0이 되도록 하면 됩니다.
이때 모든 행에서 평균값이 빠져야 되니까 인덱스를 사용해서 값을 빼주어야 합니다.

[그림 4] 평균 중심화
그러고 나서 다시 기술 통계치를 확인해보면

[그림 5] 센터링 후 기술통계치
모두 평균이 0 되었고,
아까 이야기했던 평균, 평균보다 높은 집단, 평균보다 낮은 집단을 구분할 때에는 표준편차를 사용합니다.
-1 표준편차, 평균, 1 표준편차 값을 사용하여 이 범위에서 조절 효과가 있는지 확인하는 작업이 되겠습니다.
일단 아까 세팅해둔 조절효과 분석을 해볼까요??

[그림 6] 조절효과 분석 결과
아;;; 절편이 통계적으로 유의하지 않는 신기한(?) 결과가 나왔네요 ㅋㅋㅋ
하지만 나머지 변수들은 모두 통계적으로 유의하게 나왔습니다.
이 결과에 따라서 회귀식으로 표현하면
1---------사회적위축 = 0.012 + 0.65*우울 + 0.09*학업무기력 - 0.12(우울*학업무기력) + e
이 식을 조절 효과가 드러나게 살짝 바꿔주면
2-------- 사회적위축 = 0.012 + 0.09*학업무기력 +(0.65-0.12*학업무기력)*우울 + e
(위 회귀식의 숫자를 기억해주세요!)
이렇게 하면 원래 우울의 기울기인 0.65에 학업 무기력에 따라 영향을 주고 있음을 (-0.12) 나타날 수 있습니다
학업 무기력이 높을수록 우울에 영향력을 주어 사회적 위축이 감소하는 것으로 나타났네요ㅎㅎ
-------------------------------------------------------------------------------------------------------------------------------
2. 조절 효과 그래프 그리기
이제 그래프를 그려보겠습니다.
과정이 살짝 복잡한데요..ㅎㅎ
표준편차 단위 안에서 비교를 하기 위해 각 변수의 표준편차 값을 사용합니다.
먼저 조절 변수의 표준편차 값을 활용하여서
-1 표준편차, 평균. +1 표준편차 그래프를 그립니다.
이를 위해 학업 무기력의표준편차 0.52를 사용해서 벡터를 따로 만듭니다.

[그림 7] 학업 무기력 표준편차
그러고 나서 회귀계수를 사용하여 회귀식을 따로 만들어주어야 합니다.
coef [숫자]를
최초 만들었던 (1번회귀식) 숫자가 4개가 등장합니다. 절편, 우울, 학업무기력, 우울*학업무기력
이것을 확인해보면


[그림 8] 회귀계수 확인
1: 절편
2: 우울의 회귀계수
3: 학업무기력의 회귀계수
4: 우울*학업무기력 상호작용항의 회귀계수
모든 회귀계수를 하나의 벡터에 담고
기울기와 상수항을 계산합니다.
여기서 만드는 회귀식은 2번 회귀식을 만드는 작업입니다.

[그림 9] 회귀식 만들기
coef : 모델 4(조절 효과 분석한 모델)의 모든 회귀계수 입력
labels <- as.character(H) : 그래프의 레이블을 위해 만들어줍니다.
c <- rainbow(length(H)) : H벡터의 길이만큼 색깔을 넣습니다(이 역시 그래프를 위해 미리 만들었습니다)
I : 상수항 + 학업무기력회귀계수*표준편차 벡터
S: 우울 회귀계수 + 상호작용항회귀계수*표준편차 벡터
이렇게 만들게 되면 기울기가 총 3개가 등장합니다.
이 기울기들을 따로 데이터 프레임으로 만듭니다.

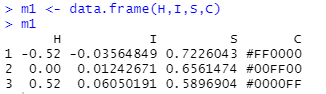
[그림 10] 기울기 데이터 프레임
아 색깔도 같이 담아서 만들었습니다 ㅎㅎ
이제 ggplot2 패키지를 사용해서 그래프를 그려줍니다.

[그림 11] 그래프 그리기 코드 1
처음 데이터 사용했던sample2 사용, x축은 우울, y축은 사회적 위축으로 설정, 값마다 점을 표시합니다.

[그림 12] 그래프 그리기 1
여기에 선을 그어야겠죠?
아까 설정한 m1graph+ 를 꼭 해주어야 전에 작업한 것 위에다가 선을 그어 놓습니다!

[그림 13] 그래프 그리기 코드 2
+geom_abline(data=m1): 아까 기울기들 따로 데이터 프레임 만든 것을 사용합니다.
aes(slope= S, intercept=I, colour=C)): slope = S 기울기는 S 벡터 사용, intercept = I, 절편은 I벡터, colour =C 색깔은 C벡터 사용

[그림 14] 그래프 그리기 2
오 선이 3개가 그어졌습니다.
저 범주의 이름을 바꿔야겠네요

[그림 15] 그래프 그리기 코드 3
역시 m1graph + 해서 계속 작업해줍니다.
+scale_color_discrete(labels=labels1) : 색깔의 이름은 labels1 벡터를 사용
+labs(colour= "helpless") : 범주 이름을 "hlepless" 로 변경

[그림 16] 그래프 그리기 3
음 이제 x축과 y축도 표준편차 단위에서만 볼 수 있도록 바꿔줍니다.
m1graph <- m1graph+ scale_x_continuous(limits = c(-0.61, 0.61))+scale_y_continuous(limits = c(-0.71,0.71))
+ scale_x_continuous(limits = c(-0.61, 0.61)): x축의 범위를 -0.61,0,0.61 로 바꿉니다.
+scale_y_continuous(limits = c(-0.71,0.71)): y축의 범위를 -0.71,0,0.71로 바꿉니다.
위 숫자들은 각각 우울, 사회적 위축의 표준편차입니다.

[그림 17] 그래프 그리기 4
그러면 각 0을 중심으로 표준편차 단위에서 어떤 효과가 나타나는지 확인할 수 있습니다... 그런데
아.. 저 레이블이 반대로 되어있습니다.
0을 중심으로 보면 절편 값이 파란색이 0보다 밑에 있는데 왜 + 값일까요..ㅎㅎ
파란색이 -0.52값이고, 빨간색이 +0.52값인데.,,, 이름을 바꿔줘야 겠네요...ㅎㅎ
다시 벡터를 만들어 줍니다 거꾸로!

[그림 18] 레이블 이름 바꾸기1
그리고 그래프를 다시 그려줍니다..처음부터 ㅎㅎㅎ

[그림 19] 그래프 그리기 코드 종합
여기서 labels=labels1 로 변경을 하면 됩니다.
그러면 드디어... 그래프가,,,!

[그림 17] 그래프 그리기 마무리
어우 세상 복잡하네요;;;ㅋㅋㅋ
학업 무기력이 높은 집단이 사회적 위축이 더 높은 것으로 나타납니다ㅎㅎㅎ
이렇게 조절 효과 분석을 마무리하겠습니다.
감사합니다!
'교육통계 > Rstudio' 카테고리의 다른 글
| 교육통계 R랑가몰라 6. 분산분석 (0) | 2022.11.02 |
|---|---|
| 교육통계 R랑가몰라 5. t-test (0) | 2022.11.02 |
| 교육통계 R랑가몰라 4. 조절효과 1) 범주형변수 (0) | 2022.11.02 |
| 교육통계 R랑가몰라 3. 매개효과분석 (0) | 2022.11.02 |
| 교육통계 R랑가몰라 2. 기초통계 - 4) 다중회귀분석2 (0) | 2022.11.02 |