안녕하세요 이번에는 분산분석에 대해서 알아보려 합니다.
분산분석은 평균값이 3개 이상이 있는 값들에 대해서 차이가 있는지 없는지 분석할 때 사용하는 방법입니다.
종속변수는 연속변수이고, 독립변수는 범주형 변수일 때 사용할 수 있겠죠
구체적으로 A, B, C 집단이 있을 때 각 집단별로 평균의 차이가 있는지
이것을 가설을 통해서 표현을 하면
영가설: A, B, C 집단의 00에 평균 차이가 없다.
대립 가설: A, B, C 집단의 00에 평균 차이가 있다.
영가설을 만족되었을 때의 수식은 A = B = C
영가설이 기각되었을 때는 등호가 단 하나라도 성립이 안 되는 것을 의미합니다.
그러니까
위 세 가지 모두 영가설이 기각되는 상황입니다.
꼭 모두 차이가 있지 않고 하나라도 차이가 발생하면 영가설이 기각되는 것이죠
-------------------------------------------------------------------------------------------------------------------------------
1. 분산분석 연습
이번분석에서는 학교가 위치한 지역별로 학생들의 학업열의에 차이가 있는지 알아보기 위해 분산분석을 사용해보겠습니다.
지역은 1: 대도시 2: 중소도시 3; 읍면지역으로 코딩이 되어있습니다.
학업열의는 평균을 내어서 변수를 만들고요
이렇게 늘 그랬듯이 변수를 만들어줍니다 ^ㅎ^

[그림 1] 학업열의 변수 만들기
여기서 이전까지 해왔던 것과 다른 것은
집단변수를 만들어주는 것인데요
집단변수는 factor로 만들어주어야 합니다. 그렇지 않으면 나중에 분석에 사용하는 함수에서 인식을 못하거나 오류 메시지가 발생합니다.
factor로 만드는 것은 어렵지 않습니다.
as.factor(데이터) 이러면 끝입니다ㅎㅎ
펙터로 변환하면서 같이 데이터프레임으로 따로 저장을 해보겠습니다.

[그림 2] 집단 변수 만들기
이렇게 변수를 만들고 나면

[그림 3] 데이터프레임 생성
이름이 그닥 예쁘지 않네요 ㅋㅋ 바꾸겠습니다

[그림 4] 변수 이름 변환
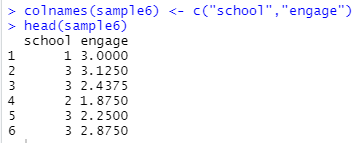
[그림 5] 이름 변환 후
학교급은 school로
학업열의는 engage로 바꿉니다.
str함수를 사용해서 구조도 잠깐 볼까요

[그림 6] 데이터 프레임 구조 확인
school은 factor로 변환이 잘 되어있고, 범주는 1,2,3으로 정해진 것을 확인할 수 있습니다.
분산분석을 시작하기 전에 먼저 등분산 가정을 만족해야 합니다.
각 세 집단의 분산이 동일한지, 이 때 사용하는 함수는 car패키지 내장함수인 levenTest를 사용합니다.
car패키지는 Rstudio 내장 함수여서 따로 설치는 안 해도 되고
library(car)로 바로 불러옵니다.
그리고 levenTest( y = 종속변수, 독립변수) 이렇게 맞춰서 입력하면 됩니다.
이 때 가설은
영가설: 집단 간 분산이 동일하다
대립 가설: 집단 간 분산이 동일하지 않다
가 되겠습니다.

[그림 7] leven test

[그림 8] leventest 결과
다행히 등분산 가정은 만족하네요ㅋㅋ 유의 확률 0.804로 영가설을 채택합니다.
그리고 이제 분산분석을 위해서 aov함수를 사용합니다.
aov(종속변수 ~ 독립변수, data = 데이터셋)
이거에 맞춰서 입력하면
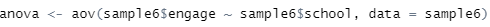
[그림 9] 분산분석
anova라는 객체에 분산분석 결과를 담아서 summary함수를 사용해서 결과를 보겠습니다.
summary(anova)

[그림 10] 분산분석 결과
아... 통계적으로 유의하지 않네요..ㅋㅋㅋ 모든 집단 간 차이가 없는 것으로 나타났습니다.
-------------------------------------------------------------------------------------------------------------------------------
2. 사후분석
지금 결과는 어. 모든 지역별로 차이가 없는 것으로 나타났는데요 ㅋㅋㅋ
그래도 이제 집단 간 차이가 어디서 얼마나 나는지 궁금할 수 있잖아요.. 만약에 차이가 있다면?
각 집단 별로 얼마나 차이가 나는지 , 그 차이는 통계적으로 유의한 지 확인하기 위해서 사후 분석을 실시합니다.
많이 사용하는 방법들이 이제 Fisher LSD, Bonferroni, Tuckey HSD 이렇게 사용하는 것 같아요
취향(?)에 따라 사용하시면 될 것 같고요 ㅋㅋㅋ
친절한 R패키지 개발자는 이 3가지를 한 번에 사용할 수 있도록 도와주었네요ㅋㅋㅋ
사용하는 패키지는 DescTools 입니다.
install.packages(DescTools)
library(Desctools) 불러오신 다음
PostHocTest(분산분석결과, method = "00")
분산분석결과에는 아까 분산분석 실시한 것을 담은 객체를 넣으면 되고
method = " 00" 에는 사용하고자 하는 사후 분석방법을 넣으면 됩니다.
"lsd" : Fisher LSD
"bonferroni" : Bonferroni
"hsd" : Tuckey HSD

[그림 11] 사후분석 실시
그러면 결과는

[그림 12] 사후분석 LSD

[그림 13] 사후분석 bonferroni

[그림 14] 사후분석 Tuckey hsd
네 모두 유의한 차이가 없는 것으로 결과가 나옵니다.
차이 값에도 분석방법에 따라 크게 차이는 없어 보인에요 ㅋㅋㅋ
이렇게 되면 결과는
대도시, 중소도시, 읍면지역 학교의 중학생 학업열의는 차이가 없는 것으로 나타났다.
로 결론이 되겠네요.
차이는 업지만,. 그래도 정리를 해볼까요 ㅎㅎ
기술을 위해 각 집단별로 분류해서 기술 통계치를 뽑겠습니다.
t-test에서 사용했던 subset함수 여기서도 사용합니다 ㅎ

[그림 15] 집단별 분류
마찬가지로 describe함수로 기술 통계치 확인하구요

[그림 16] 기술통계
기술통계치 값 확인해서 표로 정리하면 이렇게 될 것 같습니다.

사후 분석에 만약 유의한 차이가 있었다면 어떤 방법을 사용하였고,
어떤 것이 차이가 있었는지 부등호로 표시해주면 될 것 같아요
예를 들면, a <b <c라든가
a <c 라든자.. 네..ㅋㅋ
이상으로 분산분석에 대해 알아보았습니다.
감사합니다!
'교육통계 > Rstudio' 카테고리의 다른 글
| 교육통계 R랑가몰라 7. 로지스틱 회귀분석-2(분석) (0) | 2022.11.02 |
|---|---|
| 교육통계 R랑가몰라 7. 로지스틱 회귀분석-1 (이론..?) (0) | 2022.11.02 |
| 교육통계 R랑가몰라 5. t-test (0) | 2022.11.02 |
| 교육통계 R랑가몰라 4. 조절효과 2) 연속형변수 (0) | 2022.11.02 |
| 교육통계 R랑가몰라 4. 조절효과 1) 범주형변수 (0) | 2022.11.02 |