센터는 중요하다
테란 커멘드센터 날라가면 GG 쳐야 되고
아이돌 그룹의 센터가 중심을 잡아줘야 하고
야구에서 센터라인이 부실하면 수비가 개 XX 이라는 거고
(여전히 이글스는 이게 안되고 있지 ㅋㅋ 중견수 빨리 데려와..)
축구에선 센터링, 양질의 센터링을 올리면 공격수가 쉽게 슈팅 찬스를 잡듯이
(이강인 만세)
회귀모형에서도 센터링은 중요하다
(이말하려고 헛소리 살짝 지껄여봄)
앞서 다루었던 회귀모형에서 센터링을 다룬 적이 있었다.
센터링의 주된 이유로는 '절편'의 해석
독립변수가 '0'일 때 종속변수 절편이 해석이 되는데
이분형 변수가 아니고서야
독립변수가 '0'이 의미를 가질 수 있는 게 무엇이 있을까
독립변수가 소득이라면,
소득이 0에 딱 맞는 사람이 집계되기란 쉽지 않겠지
그래서 센터링 즉, 중심화를 한다.
평균을 중심으로 중심화를 하면
절편의 의미는 독립변수가 '평균'일 때 갖는 값으로 변화한다.
그럼 다층구조에서는 센터링을 어떻게 하는가
1. 다층구조의 센터링
지금 다루고 있는 주제에선
2개의 층으로 구조화되어 있다
1수준과 2수준
그래서 센터링 방법도 2가지로 할 수 있다
전체 평균 중심화 grand-mean centering
집단 평균 중심화 group-mean centering
전체 평균 중심화는 말 그대로 전체적인 수준에서의 평균으로 중심화한 것
집단 평균 중심화는 각 집단별 평균으로 중심화한 것으로 보면 된다
예를 들어보면
2개의 학교, 각 학교별 5명씩 있다고 생각하면,
|
학교
|
학생
|
점수
|
|
1
|
a
|
3
|
|
b
|
4
|
|
|
c
|
2
|
|
|
d
|
5
|
|
|
e
|
1
|
|
|
2
|
가
|
2
|
|
나
|
2
|
|
|
다
|
2
|
|
|
라
|
3
|
|
|
마
|
4
|
이런식의 구조일 텐데,
각각 '집단별'평균을 구하면
|
학교
|
학생
|
점수
|
집단평균
|
|
1
|
a
|
3
|
3
|
|
b
|
4
|
||
|
c
|
2
|
||
|
d
|
5
|
||
|
e
|
1
|
||
|
2
|
가
|
2
|
2.6
|
|
나
|
2
|
||
|
다
|
2
|
||
|
라
|
3
|
||
|
마
|
4
|
1번 학교는 소속 학생 5명(a,b,c,d,e)를 사용해서 평균을 구하면 3이 나오고
2번 학교는 소속 학생 5명(가,나,다,라,마)를 상요해서 평균을 구하면 2.6이 나온다
여기서 집단 중심 평균화를 하면
각 소속집단의 평균만큼 개별 학생 값에서 빼주면 된다
|
학교
|
학생
|
점수
|
집단평균
|
집단평균
중심화 |
|
1
|
a
|
3
|
3
|
0
|
|
b
|
4
|
1
|
||
|
c
|
2
|
-1
|
||
|
d
|
5
|
2
|
||
|
e
|
1
|
-2
|
||
|
2
|
가
|
2
|
2.6
|
-0.6
|
|
나
|
2
|
-0.6
|
||
|
다
|
2
|
-0.6
|
||
|
라
|
3
|
0.4
|
||
|
마
|
4
|
1.4
|
이러면 집단 평균 중심화한 값이 나오게 된다
그러면 전체 평균 중심화는?
전체 학생 10명을 대상으로 평균을 낸 다음
그 값을 빼주면 된다
|
학교
|
학생
|
점수
|
전체평균
|
집단평균
중심화 |
|
1
|
a
|
3
|
2.8
|
0.2
|
|
b
|
4
|
1.2
|
||
|
c
|
2
|
-0.8
|
||
|
d
|
5
|
3
|
||
|
e
|
1
|
-1.8
|
||
|
2
|
가
|
2
|
-0.8
|
|
|
나
|
2
|
-0.8
|
||
|
다
|
2
|
-0.8
|
||
|
라
|
3
|
0.2
|
||
|
마
|
4
|
1.2
|
2. 이게 무슨 의미가 있니
그래서 이걸 왜 하냐
1수준과 2수준을 분리를 해서 투입하는 회귀분석이라
그럼 각 수준별 분산에만 영향을 주고 있지 않나 생각할 수 있다
1수준 변수 투입하면 1수준 분산에만 영향을 주고
2수준 변수 투입하면 2수준 분산에만 영향을 준다던가
하지만 여전히 서로 영향을 주고 받고 있는 관계인지라
변수 투입에 따라 분산이 영향을 받는다
이걸 어케 아느냐?
상관을 보면 알 수 있다
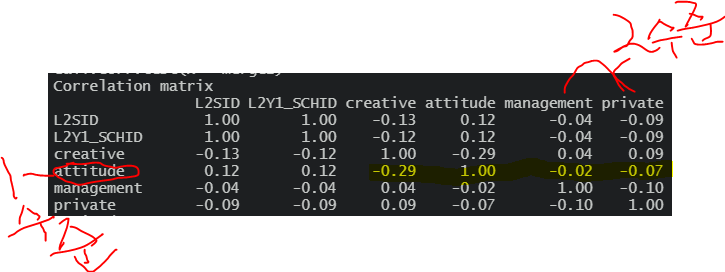
중심화를 하지 않은 1수준 변수가 2수준 변수와 상관이 존재하는 것이 확인 가능하다
그렇기 때문에
1수준, 2수준 변수일지라도 각각의 분산에 영향을 줄 수 밖에 없다
전체평균중심화를 하면 어떨까?
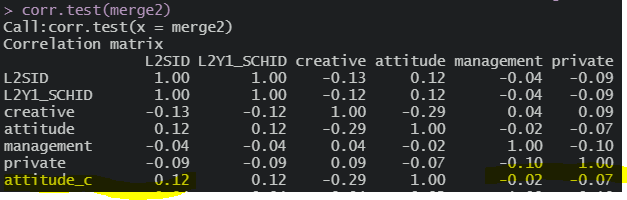
여전히 상관이 존재한다
그럼 집단중심평균화를 한다면?
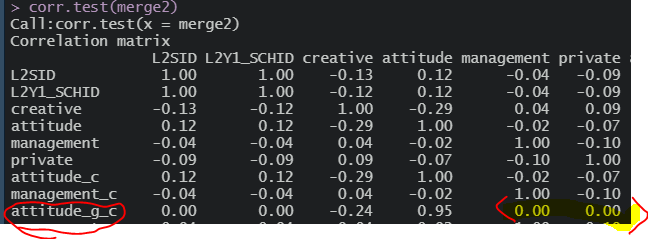
집단 평균 중심화를 하면 2수준 변수와의 상관이 사라진다(오호라..)
정리하면,
1수준 변수를 전체평균 중심화를 하고 분석하게 되면
2수준 변수와 상관이 남아있기 때문에,
1수준 변수의 회귀계수 해석은 정확하게 1수준만의 영향을 의미하지 않는다
영향이 혼재되어 있다
반면, 1수준 변수를 집단평균 중심화를 하고 분석하면
2수준 변수와 상관이 남아있지 않기 때문에
1수준 변수의 회귀계수는 1수준만의 효과라고 해석할 수 있게 된다
그래서 연구자가 다층모형을 적용하고자 할 때,
본인이 어떤 수준의 변인에 관심이 있는지에 따라
중심화 적용을 차별적으로 가져가야 한다
다시 한 번 정리하면,
관심 변수가 연속변수일 때,
① 1수준 변수에 관심: 1수준 변수를 집단 평균 중심화를 할 것
② 2수준 변수에 관심: 1수준 변수를 전체 평균 중심화를 할 것
③ 층위간 상호작용 효과 관심: 1수준 변수를 전체 평균 중심화를 할 것
정도로 볼 수 있지 않을까?
만약 관심 변수가 이분형 변수면 굳이 굳이 센터링은 안 해도 될 것 같고
2수준에서는 집단평균 중심화란 없다
애초에 2수준 자체가 각각의 집단인데
그래서 2수준에서는 전체평균중심화만 하면 된다
3. 그래서 어케함?
데이터 핸들링은 R이 편해서 일단 R로 해보면 ㅋㅋ
3-1. 전체평균 중심화
전체 평균 중심화는 쉽다
데이터셋에서 평균값 산출해서 각각 빼주면 되니까
merge$attitude_c <- merge$attitude-mean(merge$attitude, na.rm = T)
데이터$중심화변수 <- 데이터$원래변수 - 평균값
그럼 집단 중심 평균화는?
tidyverse 도와줘..!
group_by 함수를 사용한다
merge %>%
group_by(L2Y1_SCHID) %>%
mutate(attitude_g_c = attitude - mean(attitude, na.rm = T)) -> merge2
데이터 %>%
group_by(2수준ID) %>%
mutate(집단중심평균 변수 = 원래변수 - 평균값)
이러고 잘 됐나 확인해보면,
일단 전체 평균값 확인
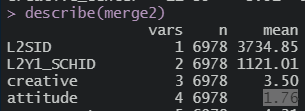
1.76
학교 하나 뽑아서 해당 학교의 평균값 확인
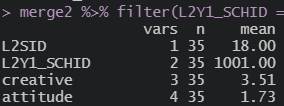
1.73
센터링 후 데이터 확인

1번 학생 원래 값이 2였고
전체 평균 중심화 (attitude_c) 2-1.76 = 0.240
집단 평균 중심화 (attitude_g_c) 2-1.73 = 0.274
(이건 아마 라운딩 때문일 것이라, R 계산이 정확할 듯)
4. 분산값에도 변화가 있는가?
도 확인해봐야겠ㅈ..
먼저 전체 평균 중심화 변수를 넣었을 때
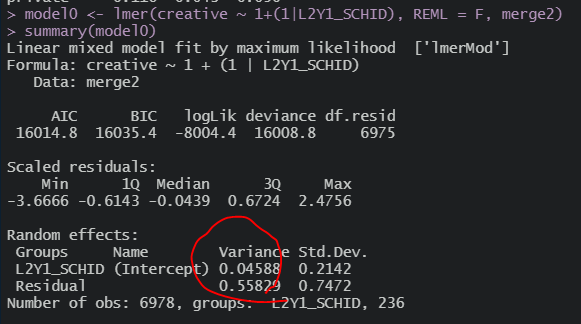
초기 분산값에서
1수준 변수 투입
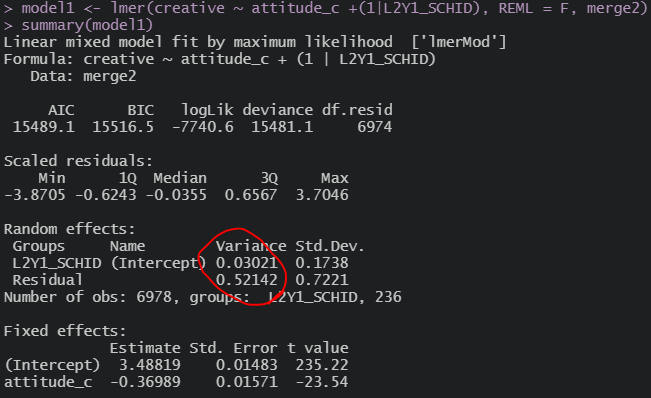
전체 변수 투입
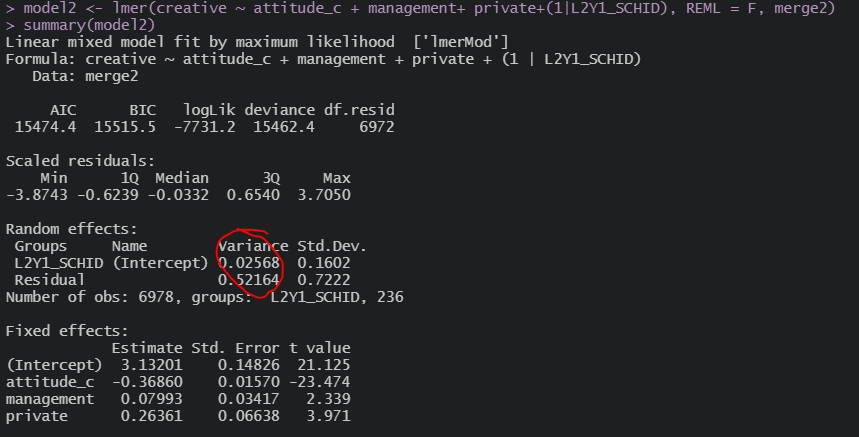
1, 2 수준 분산 모두 움직인다
이번엔 집단 평균 중심으로 넣어보면
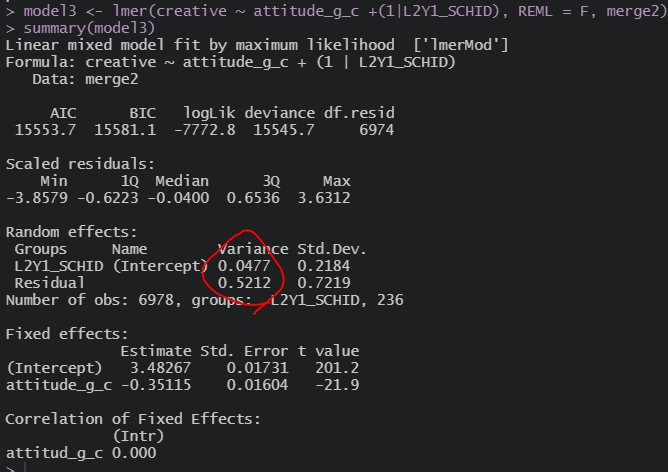
model0이랑 비교하면 오히려 2수준 분산이 줄어들긴 커녕 살짝 늘어났네ㅋㅋ
그리고 이제 2수준 변수 넣으면
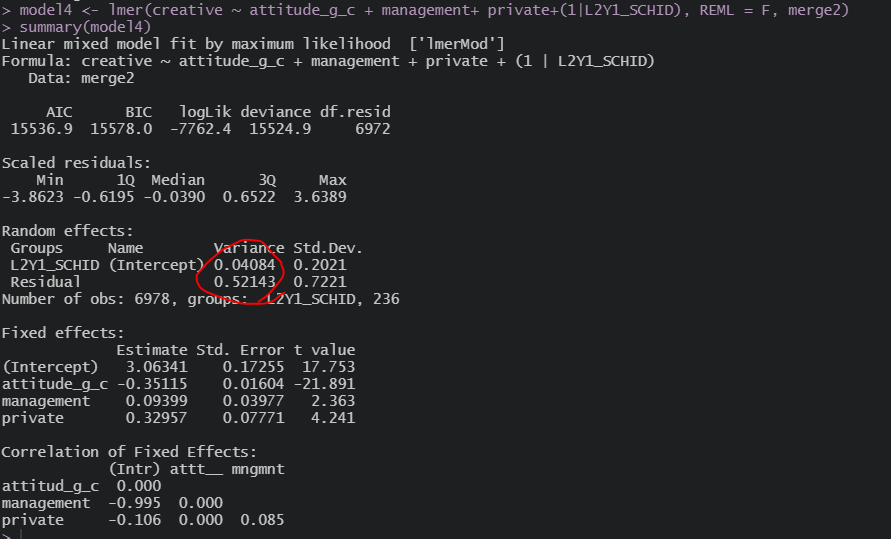
이제서야 2수준 분산이 줄어든 것을 볼 수 있다
4. 다층모형 역시 센터가 중요하다
연구 모형, 투입 변수가 어떻게 작용하고
해석할 수 있는지는
꼭 면밀히 확인해야 한다
이를 위해 센터링은 꼭 필요함을 강조해보았다
혹시 더 자세한 내용을 원한다면
Enders, C. K., & Tofighi, D. (2007). Centering predictor variables in cross-sectional multilevel models: a new look at an old issue. Psychological methods, 12(2), 121.
이 논문을 찾아보심이..
다음장은.. 종단 모형?
'교육통계 > 다층모형' 카테고리의 다른 글
| 다층모형- 4.횡단모형(STATA) (0) | 2023.09.06 |
|---|---|
| 다층모형 - 3.데이터생성(STATA) (0) | 2023.09.06 |
| 다층모형- 4.횡단모형(R) (0) | 2023.09.06 |
| 다층모형 - 3.데이터생성(SPSS) (0) | 2023.09.04 |
| 다층모형 - 3.데이터생성(R) (0) | 2023.09.04 |