아주 간단한 횡단모형을 분석해보자
학생들의 창의성에 수업태도(1수준), 운영방식(2수준), 설립유형(2수준)이 유의한 영향을 주는가?
저번에 만들었던 통합데이터로 시작~
1. 기술통계
아 일단 기술통계는 슬쩍 확인하고 가야겠지?
R로 기술통계 내는데 원톱은 아무래도 psych 패키지
일단 그전에
case_when으로 더미변수 변환할 때,
numeric이 character로 바뀌었으니
다시 numeric으로 돌려~
clean_data %>%
mutate(private = as.numeric(private)) -> clean_data
이렇게 돌린다음에.
describe 함수로 기술통계 확인

근데 그냥 돌리면 학생 ID와 학교 ID도 모두 기술통계에 포함되서 쫌 뵈기 그렇다
그러니, 이 놈들은 제외해주고

describe(clean_data)[3:length(clean_data),]
인덱스를 활용해서 위 두 개는 잘라 버리자
그리고 생각해보니
학교 수준 변수(운영방식, 설립유형)은 2수준 변수니까
N이 저렇게 많이 나오면 안되겠지..
group_by와 select, unique를 조합해서
학교 수준 데이터만 기술통계를 따로 내보자
어떻게?
clean_data %>%
group_by(L2Y1_SCHID) %>%
select(L2Y1_SCHID, management, private) %>%
unique() %>%
describe()
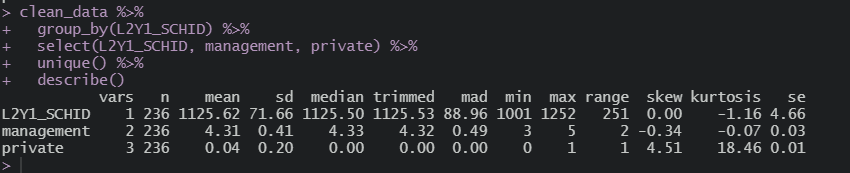
이렇게 되면,
학생 수준 데이터는 총 6,978 / 학교 수준 데이터는 236개인 것으로 확인된다
2. lme4를 써보자
다층모형을 지원하는 패키지 중 하나인 lme4
install.packages 로 설치하고
불러오자

이제 lmer 함수를 써서 모형을 분석해나가면 된다
2-1 무조건 모형
무조건 모형은
종속변수만 넣은 채, 분석하는 것으로
바로 아래 모형의 상태에서 분석하게 되는 것

이 구조를 적용한 수식을 작성해서 lmer 함수에 넣으면 된다
model <- lmer(종속변수 ~ 1 + (1|2수준_key변수), data, REML = T)
여기서 REML은 모형 추정 방식을 뜻하는데,
REML : Restricted Maximum Likelihood 제한최대우도
REML = F 로 놓으면 ML로 분석
Maximum Likelihood 최대우도(아마도 완전최대우도 일 것 같긴 한데.. 일단)
아직 이 두 가지 추정방법에 대해 완전히 이해가 되지 않은상태라..
잘은 모르겠지만,
ML이나 REML 이나 추정치에서 차이는 크게 없다고 한다
(다층모형분석, 2023, 김준엽, 박현정, 신혜숙 공역, 학지사)
일단 디폴트가 REML = T라서
신경쓰지 말고 돌려보도록 하자

이렇게 돌리고 summary 돌려주면
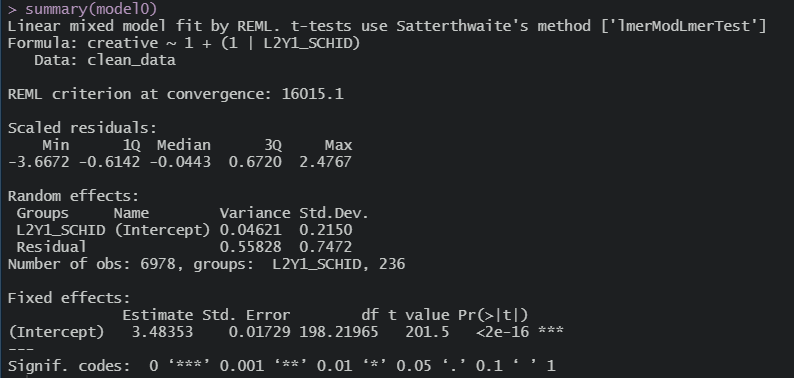
결과표가 짜잔
분리해서 보면, 먼저 분산
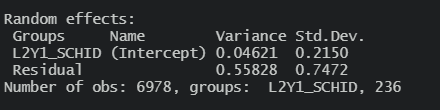
2수준 분산: 0.04621
1수준 분산: 0.55828
이 구해졌기에 ICC를 바로 계산할 수 있다
ICC는?

그냥 있는 숫자 써서 계산해도 괜찮긴 하지만
ICC <- 0.04621/(0.04621+0.55828)
VarCorr 함수를 활용해서 df 만들어서 계산하는 것도 나쁘지 않지
var.cov <- as_tibble(VarCorr(model0))
var.cov$vcov[1]/sum(var.cov$vcov)
아무튼 이렇게 계산하면
ICC 값은 0.07644461, 약 7%
2수준 분산이 전체분산 중 7% 정도를 차지 하고 있다
그러니 2수준 넣어볼만 한 듯??
2-2 일단 1수준 투입한 모형
1수준 변수였던 수업태도를 추가해주면
model1 <- lmer(creative ~ attitude +(1|L2Y1_SCHID), clean_data)
종속변수 ~ 1수준 변수 + 1수준변수2 ..
이렇게 써주면 되나, 일단 1수준 변수 1개니까
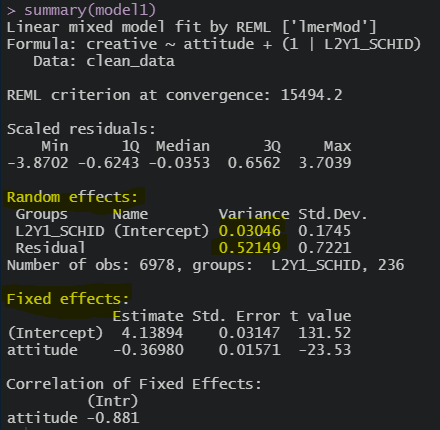
분산(random effects)부터 보면, 2수준과 1수준 모두 감소한 것을 볼 수 있다
회귀계수(fixed effects)를 보면 수업태도가 추가되면서
절편값에 변화가 생겼다. 오..
두 값 모두 통계적으로 유의하고,
바로 기냥 2수준 변수도 넣어보자
2-3 2수준 변수 투입해서 최종모형 완성
2수준 변수라고 특별히 따로 추가적인 작업이 필요하거나 그렇진 않다
그냥 1수준 변수 옆에 자연스럽게 써주면 된다
model2 <- lmer(creative ~ attitude + management+ private+(1|L2Y1_SCHID), clean_data)
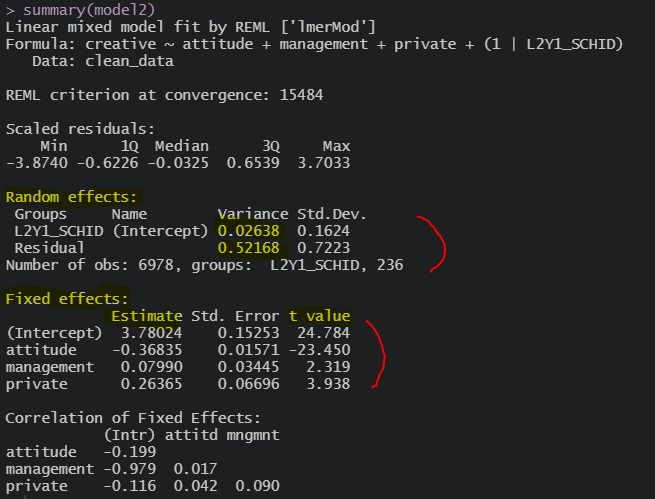
2수준까지 투입하고 보면,
분산이 상당히 줄어들었다는 것과
회귀계수들 값도 한 번 상당히 조정된 것을 볼 수 있다
신기하네 다 유의수준 통과했네;;ㅋㅋ
이 결과대로 일단 해석하면, 국립에비해 사립학교 학생들의 창의력이 .26만큼 높고,
수업태도 나쁠 수록 창의력이 높고, 운영관리 열심히 할 수록 창의력이 높아지는
교장선생님들 참 좋아할 결과가 나왔다 ㅋㅋ
계수는 그렇다 치고 모델 괜찮은지는 어떻게 암
3. 모델 test
방법 1. 정보지수 활용
R에서 정보지수(AIC, BIC)를 산출해서 비교하는 방법이 있다
정보지수는 작을 수록 적합하다고 보는 것이니,
변수를 모형에 추가할 때, 정보지수가 어떻게 움직이는지 확인하면 되는데,
방법은 그냥 AIC, BIC 내장 함수 이용하면 바로 계산 가능하다
AIC(모델)
BIC(모델)
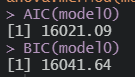

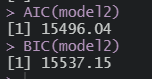
음..BIC가 애매한데
뭐 일단은;;ㅋㅋ
방법 2. 모델간 ANOVA
회귀분석에서 모형 anova 하듯이
ANOVA를 돌려준다
그럼 원래 비교해야 하는 기본 모형은
단순선형회귀에서 시작한다
그것을 위해 lm 함수로 선형회귀 하나 만들어주고
model_base <- lm(creative ~ 1, clean_data)
summary(model_base)
anova함수 사용해서 모델 비교
anova(모델1, 모델2)
lm쓴 모델을 앞에다 쓰면 왜인지 이런 에러가 뜨는데...

그래서 순서를 바꿨더니
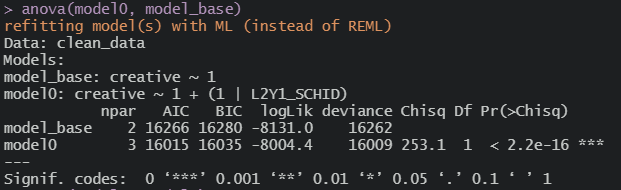
돌아간다
anova가 REML을 안 좋아하나보다.. ML로 해야 모형간 비교가 되는군
(우도기반 전체 카이제곱 검정을 위해선 ML이 필요하다는 군요
출처: 다층모형분석, 2023, 김준엽, 박현정, 신혜숙 공역, 학지사)
선형보다 다층해도 괜찮겠네~
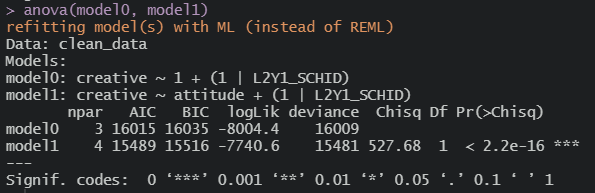
1수준 변수 넣은 모델도 괜춘하네~
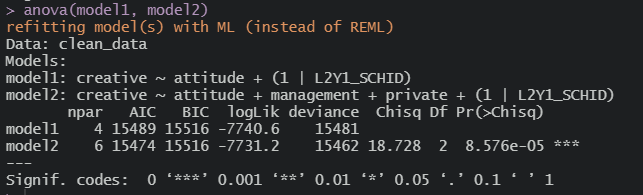
2수준 넣어도 뭐 괜찮구만 ㅋㅋ
최종모형은 1+2 수준 변수 넣은 모형으로 결정해보도록 하자
그래서 결과표로 어째어째 정리하면~
4. 결과 정리
여지껏 나온 결과들을 정리하면
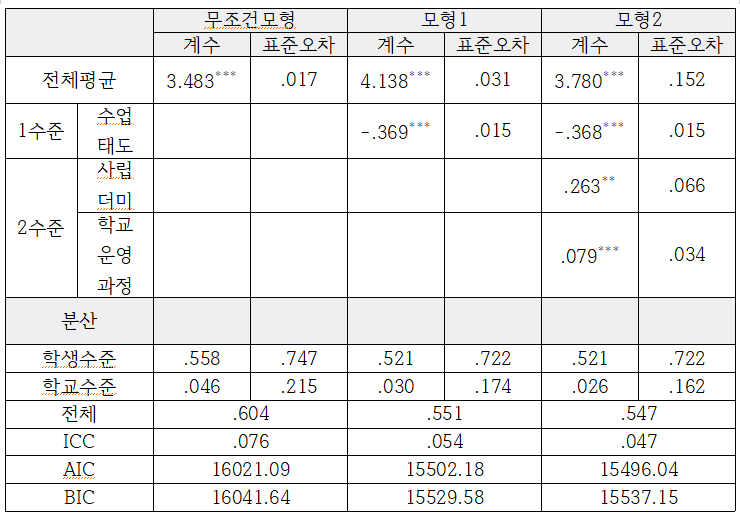
오 뭔가 그럴듯함
회귀계수들이야 그대로 해석하면 되고,
돌리다보니 깨달은(?) 것은
어차피 모델 비교 anova 돌려야 되니까 ML로 분석하고 정리하는게 좋을 것 같고
ICC는 딱 무조건 모형에서만 원래 ICC의 의미대로 해석할 수 있다는 점만 주의하면 좋을 것 같은데
1수준 변수 투입 후 2수준 분산도 같이 줄어드는데..
이건 다음에..ㅎ
'교육통계 > 다층모형' 카테고리의 다른 글
| 다층모형- 4.횡단모형(STATA) (0) | 2023.09.06 |
|---|---|
| 다층모형 - 3.데이터생성(STATA) (0) | 2023.09.06 |
| 다층모형 - 3.데이터생성(SPSS) (0) | 2023.09.04 |
| 다층모형 - 3.데이터생성(R) (0) | 2023.09.04 |
| 다층모형 - 2.기본 구조 (0) | 2023.09.04 |