잠재성장모형에 이어
또 다른 종단 분석방법을 살펴볼까요.
자기회귀교차지연모형입니다.
1. 간단한 이론..?

예시 모형에서 보다시피 여러 시점에서 측정된 변수들 간의 관계를 살펴봅니다.
특정 시점의 변수가 다른 시점의 변수에 어떻게 영향을 주는지 볼 수 있겠죠?
이 모형의 장점은 시간 관계 안에서 변수들의 관계를 살펴보는 것입니다.
간단하게(?) 보이는 모형에
여러 단계를 거쳐야 하는 귀찮음이 있지만
그래도 잘 연습하면 유용한 분석 모형이 될 것이라 생각됩니다.
거쳐야 하는 단계는 측정 동일성 -> 경로 동일성 -> 오차 공분산 동일성을 검정을 하고 난 다음
최종 모형이 결정됩니다.
위 예시 모형을 다시 세세하게 보면

이런 모양이 나옵니다.
측정 동일성을
X1은 x1-1, x1-2, x1-3 으로 구성된 변수입니다.
X2는 x2-1, x2-2, X2-3 으로, X3은 마찬가지로 x3-1, x3-2, x3-3 으로 구성되어 있죠.
다 같은 문항이지만, 시점이 다르게 적용되었습니다.
각 시점마다 이 문항들이 동일한 요인 부하량이 적용되는지를 확인합니다.
측정 동일성이 검증됐다는 것은 각 시점마다 동일하게 측정되고 있음을 나타내는 것입니다.
두 번째로 경로 동일성은
경로 동일성에 자기 회귀계수와 교차 지연 계수가 있습니다.
X1 -> X2 -> X3 으로 가는 동안, 화살표가 두 번 나옵니다.
이건 자기 회귀 계수로
이 화살표가 의미하는, 회귀계수가 동일하게 영향을 주는지 검증하게 됩니다.
교차 지연 계수는
X1 -> Y2,
X2 -> Y3
이렇게 교차해서 영향을 주는 계수들을 의미합니다.
세 번째로 오차 공분산 동일성은
오차(e1, e2) 공분산을 고정함으로써
시간에 의한 오차인지, 변수의 관련성에 의한 오차인지 검정하게 됩니다.
그래서 종합해서,
측정 동일성, 경로 동일성, 오차 공분산 동일성 검정을 적용한 모형들 간 적합도 지수 비교를 통해
최종 모형을 결정합니다.
모형 적합도 지수로

늘 보던.. 이 친구들을 봅니다 ㅋㅋ
2. 분석 연습
분석을 실제로 돌리면서
측정 동일성, 경로 동일성, 오차 공분산 동일성을 보려 합니다.
저번 잠재성장모형에서 사용하였던 우울과 학업 무기력 간의 관계를
자기 회귀 교차 지연 모형으로 보려 합니다.
측정 동일성부터 봐야 하기 때문에,
사실상 요인 분석부터 봐야 합니다.
그래서, 각각의 문항을 모두 살려서 가져옵니다.
m2018 <- KCYPS2018m1Yw1[,c(1:2,198:207,126:141)]
m2019 <- KCYPS2018m1Yw2[,c(1:2,203:212,131:146)]
m2020 <- KCYPS2018m1Yw3[,c(1:2,141:150,69:84)]
m2018 <- na.omit(m2018)
m2019 <- na.omit(m2019)
m2020 <- na.omit(m2020)
m_merge <- merge(m2018, m2019, by = c("HID","PID"))
m_merge2 <- merge(m_merge, m2020, by = c("HID","PID"))
이렇게 합치면, 1~3차년도의 각각의 문항들을 모두 포함시켜서 데이터를 생성할 수 있습니다.
그리고 이 패키지들을 불러오고
library(lavaan)
library(semPlot)
모형들을 하나하나 만들어갑니다.
아 그전에..
모형의 경로에 대해서 '이름'을 정해두는 것이 좋을 것 같습니다.

어질어질 하지만..
X1 -> X2 : A1
X2 -> X3 : A2
Y1 -> Y2 : B1
Y2 -> Y3 : B2
X1 -> Y2 : C1
X2 -> Y3: C2
Y1 -> X2: D1
Y2 -> Y3 : D2
X2 - Y2 오차 : E1
X3 - Y3 오차 : E2
X1 측정문항: xa1, xa2, xa3...
X2 측정문항: xb1, xb2, xb3...
X3 측정문항: xc1, xc2, xc3 ...
Y1 측정문항: ya1, ya2, ya3...
Y2 측정문항: yb1, yb2, yb3...
Y3 측정문항: yc1, yc2, yc3...
이 경로들에 대한 이름들을 잘 보신 다음 천천히 진행하면 좋습니다.
먼저 무조건 모형을 만들어줍니다.
어떠한 제약도 걸지않고 모형을 만들어줍니다.
무조건 모형은...
model0 <- 'sad1 =~ xa1*YPSY4E01w1+xa2*YPSY4E02w1+xa3*YPSY4E03w1+xa4*YPSY4E04w1+xa5*YPSY4E05w1+xa6*YPSY4E06w1+
xa7*YPSY4E07w1+xa8*YPSY4E08w1+xa9*YPSY4E09w1+xa10*YPSY4E10w1
sad2 =~ xb1*YPSY4E01w2+xb2*YPSY4E02w2+xb3*YPSY4E03w2+xb4*YPSY4E04w2+xb5*YPSY4E05w2+xb6*YPSY4E06w2+
xb7*YPSY4E07w2+xb8*YPSY4E08w2+xb9*YPSY4E09w2+xb10*YPSY4E10w2
sad3 =~ xc1*YPSY4E01w3+xc2*YPSY4E02w3+xc3*YPSY4E03w3+xc4*YPSY4E04w3+xc5*YPSY4E05w3+xc6*YPSY4E06w3+
xc7*YPSY4E07w3+xc8*YPSY4E08w3+xc9*YPSY4E09w3+xc10*YPSY4E10w3
helpless1 =~ ya1*YINT2B01w1+ya2*YINT2B02w1+ya3*YINT2B03w1+ya4*YINT2B04w1+ya5*YINT2B05w1+ya6*YINT2B06w1+ya7*YINT2B07w1+
ya8*YINT2B08w1+ya9*YINT2B09w1+ya10*YINT2B10w1+ya11*YINT2B11w1+ya12*YINT2B12w1+ya13*YINT2B13w1+ya14*YINT2B14w1+
ya15*YINT2B15w1+ya16*YINT2B16w1
helpless2 =~ yb1*YINT2B01w2+yb2*YINT2B02w2+yb3*YINT2B03w2+yb4*YINT2B04w2+yb5*YINT2B05w2+yb6*YINT2B06w2+yb7*YINT2B07w2+
yb8*YINT2B08w2+yb9*YINT2B09w2+yb10*YINT2B10w2+yb11*YINT2B11w2+yb12*YINT2B12w2+yb13*YINT2B13w2+yb14*YINT2B14w2+
yb15*YINT2B15w2+yb16*YINT2B16w2
helpless3 =~ yc1*YINT2B01w3+yc2*YINT2B02w3+yc3*YINT2B03w3+yc4*YINT2B04w3+yc5*YINT2B05w3+yc6*YINT2B06w3+yc7*YINT2B07w3+
yc8*YINT2B08w3+yc9*YINT2B09w3+yc10*YINT2B10w3+yc11*YINT2B11w3+yc12*YINT2B12w3+yc13*YINT2B13w3+yc14*YINT2B14w3+
yc15*YINT2B15w3+yc16*YINT2B16w3
sad2 ~ A1*sad1 + D1*helpless1
sad3 ~ A2*sad2 + D2*helpless2
helpless2 ~ B1*helpless1 + C1*sad1
helpless3 ~ B2*helpless2 + C2*sad2
sad1 ~~ helpless1
sad2 ~~ E1*helpless2
sad3 ~~ E2*helpless3'
세상 끔찍합니다 ㅋㅋㅋ
하나씩만 뜯어서 보면 금방(?) 이해할 수 있습니다.
sad1 =~ xa1*YPSY4E01w1+xa2*YPSY4E02w1+xa3*YPSY4E03w1+xa4*YPSY4E04w1+xa5*YPSY4E05w1+xa6*YPSY4E06w1+
xa7*YPSY4E07w1+xa8*YPSY4E08w1+xa9*YPSY4E09w1+xa10*YPSY4E010w1
'우울1차년도 변수는 =~ 10개의 문항으로 구성된다. ' 의미이고
앞에 붙여둔 것들은 각각의 요인 부하량에 '이름'을 붙여줬다 생각하시면 됩니다.
밑에 sad2, sad3, helpless1,2,3 도 마찬가지로 구성되어 있는 것이고
sad2 ~ A1*sad1 + D1*helpless1
우울 2차년도 변수는 우울 1차와 학업 무기력 1차의 영향을 받습니다(화살표를 받는 입장에서)
그래서 각각의 경로를 표시해주고, 아까 정해준 경로의 이름을 부여한 것입니다.
sad1 ~~ helpless1
여기서 ~~ 은 두 변수간 상관을 설정한다고 보면 되겠습니다.
이제 세상 끔찍한 이 모형을 돌려보겠습니다.
fit0 <- sem(model0, data = m_merge2)
result0 <- summary(fit0, fit.measures = T, standardized = T)
결괏값을 따로 저장해두는 것이 좋습니다.
나중에 모형 비교해야 되걸랑요..ㅋㅋ
일단 무조건 모형 결과를 살펴보면,
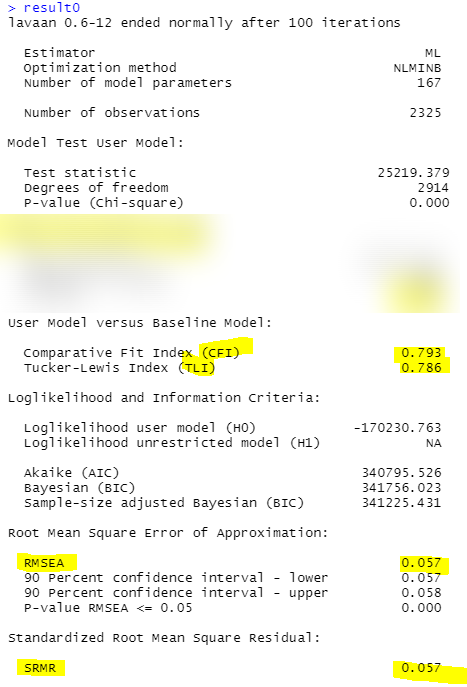
다행히 저번 잠재성장모형처럼 TLI가 마이너스가 나오거나 그러진 않았네요..(휴..)
이 정도면 오 적당히 훌륭합니다.
모델 경로에 이름을 정해준다는 게 이런 의미입니다.
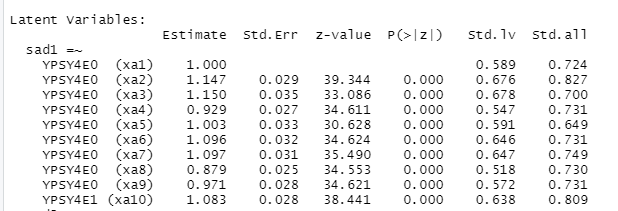
변수 옆 괄호 안에 아까 지정한 이름이 다 들어가 있습니다.
이걸로 계수들을 조작을 할 수 있게 됩니다.
일단 모델 적합도들을 먼저 비교하는 게 우선이니까,
바로 측정 동일성으로 넘어가겠습니다.
측정 동일성을 위해서는, 측정 문항들의 화살표들을 동일하다 설정해주면 되겠죠
아까 무조건 모형 뒤에다
xa1 == xb1
xa2 == xb2
xa3 == xb3
xa4 == xb4
xa5 == xb5
xa6 == xb6
xa7 == xb7
xa8 == xb8
xa9 == xb9
xa10 == xb10
xb1 == xc1
xb2 == xc2
xb3 == xc3
xb4 == xc4
xb5 == xc5
xb6 == xc6
xb7 == xc7
xb8 == xc8
xb9 == xc9
xb10 == xc10
ya1 == yb1
ya2 == yb2
ya3 == yb3
ya4 == yb4
ya5 == yb5
ya6 == yb6
ya7 == yb7
ya8 == yb8
ya9 == yb9
ya10 == yb10
ya11 == yb11
ya12 == yb12
ya13 == yb13
ya14 == yb14
ya15 == yb15
ya16 == yb16
yb1 == yc1
yb2 == yc2
yb3 == yc3
yb4 == yc4
yb5 == yc5
yb6 == yc6
yb7 == yc7
yb8 == yc8
yb9 == yc9
yb10 == yc10
yb11 == yc11
yb12 == yc12
yb13 == yc13
yb14 == yc14
yb15 == yc15
yb16 == yc16
얘네들을 붙여서 돌리면 되겠습니다.
다 따로따로 써야 합니다..
같이 썼더니(xa1 == xb1 == xc1) 이상하게 돌아가더라고요ㅋㅋ
결괏값을 보면,
fit1 <- sem(model1, data = m_merge2)
result1 <- summary(fit1, fit.measures = T, standardized = T)

무조건 모형이랑 큰 차이는 없어 보이네요,
진짜 측정이 동일하게 설정이 됐느냐는

동일하죠??
이제 모형 간 차이를 볼까요
보통 카이제곱 검정을 하긴 하는데..
카이제곱 검정이 워낙 표본수에 영향을 많이 받아서..
암튼 일단 카이제곱 검정을 위해 anova를 사용합니다.
anova(fit0, fit1)
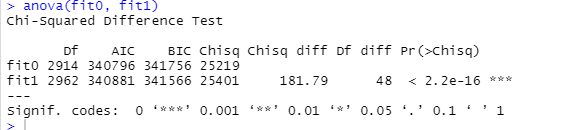
카이제곱이 통계적으로 유의하네요.. 이럼 무조건 모형을 선택하게 되지만..
이것보단 보통 CFI, TLI, RMSEA를 더 보니까..
이거랑 더불어 간명한 모형이 최고입니다ㅋㅋㅋ
아몰랑 하고
이제 경로 동일성으로 넘어가렵니다.ㅋㅋ
경로 동일성에서 자기 회귀계수(A1, A2, B1, B2)에 먼저 제약을 주겠습니다.
아까 모델 1에서
A1 == A2
B1 == B2
이거만 추가해주면 됩니다.
결과를 보면,
fit2 <- sem(model2, data = m_merge2)
result2 <- summary(fit2, fit.measures = T, standardized = T)
result2

여전히 적합도가 크게 변하지 않네요

그러니 여전히 anova도 이렇게 나오고..
아몰랑 또 넘어갑니다.
경로 동일성에서 이제 교차 회귀계수(C1, C2, D1, D2) 제약을 줍니다.
아까 모델 2에서
C1 == C2
D1 == D2
만 추가해줍니다.
fit3 <- sem(model3, data = m_merge2)
result3 <- summary(fit3, fit.measures = T, standardized = T)
result3

안 바뀌네..
경로 동일성은 잘 설정되어 있습니다.
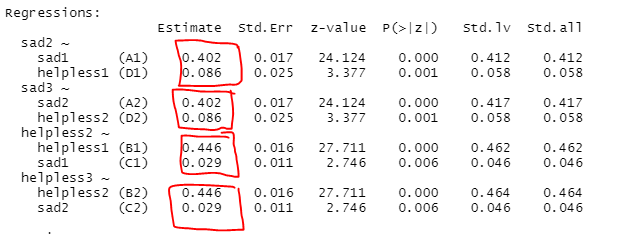
anova는 또 뻔하겠고
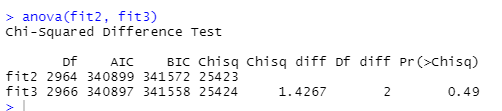
어 유의하지 않네요 오..ㅋㅋㅋㅋ
일단 또 넘어갑니다.
마지막으로 오차 공분산 설정
모델 3에서
E1 == E2
만 추가해주면 됩니다.
결과를 보면..
fit4 <- sem(model4, data = m_merge2)
result4 <- summary(fit4, fit.measures = T, standardized = T)
result4

여전히 큰 차이 없고..ㅋㅋㅋ
anova는..?

오 유의하지 않습니다ㅋㅋㅋ
그럼 그냥 마지막 모형인 오차 공분산 모형을 설정하겠다~ 명분을 만들고

동일하게 설정 잘 되어버렸고
최종 모형인, 오차 공분산 모형을 연구모형으로 채택합니다ㅋㅋㅋ
3. 결과 정리
열심히 분석했으니..
예쁘게 정리해야겠죠ㅋㅋ
측정 동일성부터 오차 공분산까지 어떻게 설정했는지 먼저 설명해줍니다.

여기에 모형 2,3,4에서 x, y변수를 또 나눠서 모형을 설정하는 것도 가능한데..
귀찮으니까.. 넘어갑시다
그다음 모형 적합도 지수를 정리해줍니다.

모형 적합도 지수를 비교했을 때, 모형적합도 지수가 크게 차이가 안 나니까
가장 간소한 모형인 모형 5를 연구모형으로 선택했다 해줍니다.
그리고 이제 추정치를 정리해줍니다.

해석은 회귀분석과 동일합니다.
마지막으로 표준화 계수를 활용해서 그림을 그려주면..

아까 모형을 살려서 색깔을 넣은 것이고..
만약 논문에 쓰실 거면 당연 흑백으로..ㅋㅋㅋ
후 이 정도면 되지 않을까 싶습니다.
'교육통계 > Rstudio' 카테고리의 다른 글
| Educational statistics Using R - 1. Descriptive statistics 4) Descriptive statistics (0) | 2022.11.09 |
|---|---|
| 교육통계 R랑가몰라 2. 기초통계 - 3) 다중회귀분석1 (0) | 2022.11.03 |
| 교육통계 R랑가몰라 9. 구조방정식(SEM) 4) 잠재성장모형 (0) | 2022.11.03 |
| 교육통계 R랑가몰라 9. 구조방정식(SEM) 3) 경로모형 (0) | 2022.11.03 |
| 교육통계 R랑가몰라 9. 구조방정식(SEM) 2) 모형검증 (0) | 2022.11.03 |