지금까지 뭔가 올렸던 것은
횡단 연구 방법이었습니다.
횡단만 다루면 조금 아쉬운 부분이 있죠
횡단 연구의 장점으로 일반적인 경향을 파악하고, 개인 간 비교가 용이한 점은 있지만
1. 개인의 성장과 발달과정을 파악하기는 어렵고
2. 분석을 통해 얻은 결과가 특정 시점에서만 유효한지, 다른 시점에서도 유효한 지 모르고
3. 변수들간 시간적 선행성 확보가 쉽지 않습니다
**참고자료: 이종승, 2009, 교육심리사회 연구방법론**
특히 이 '시간적 선행성 확보'가 쉽지 않은 점은
주로 관심 있는 '인과적 효과'를 밝히기 쉽지 않다는 점입니다.
사회과학 특성상, 실험 연구가 쉽지 않기 때문에 분석 결과를 인과관계로 표현하기 어렵고
시간적 선후관계도 불명확하다는 점이 아쉽죠.
그래서 시간에 따른 변수 간의 관계 파악을 위해 종단연구를 사용합니다.
시간적 선행성 확보를 통해 이걸로 완전히 인과관계다라고 주장하는 데는 약간 무리가 있지만,
그래도 횡단 연구에 비해 변인 간의 인관관계나 개인의 성장, 변화 양상 파악에 장점이 있습니다.
먼저 설명하고자 하는 방법은 종단연구 분석 방법 중 하나인 잠재성장모형입니다.
잠재성장모형은 전체 시점 동안 개인 내 변화 궤적을 추정하는데 장점이 있습니다.
대충 모형을 그려보면..

앞선 회귀분석이나 구조방정식과 조금 낯선 모형을 마주하게 됩니다.
□ ○ 는 구조방정식에서 내생변수, 외생변수로 쓰이긴 하는데,
갑자기 △ 가 등장합니다 ㅋㅋ
일단 이 친구는 뭘까요.
1. 평균 구조
이 친구는 '평균 구조'라고 보면 되는데, 모든 사례에 '1'이라는 상수를 부여한 것을 표현한 것입니다.
어떤 값이든 간에 1을 곱한다 한들 값이 변하지 않으니,
이론적(?), 개념적(?)으로 '1'을 눈에 보이게 표현해줍니다.
구조방정식은 공분산 구조를 활용하는 모형이라, 평균 구조를 잘 활용하지 않을 때가 많지만
잠재성장모형에서처럼 평균구조를 활용할 때가 있습니다.
어쨌든 이게 뭐냐.. 직관적으로 '평균'을 의미한다고 보면 됩니다.
회귀분석으로 설명하자면,
Y의 평균을 '평균 구조'를 활용해서 구조방정식처럼 표현할 수 있습니다.

이건 또 무슨 소리냐..
실제 데이터로 보면 이해가 될 것 같기도 합니다.
늘 사용하던, KCYP 2018의 자아존중감으로 학업열의를 예측하는 회귀를 돌려보겠습니다.
기술통계 값을 보면,

학업열의 평균은 2.47 정도
자아존중감은 2.99 정도 되네요
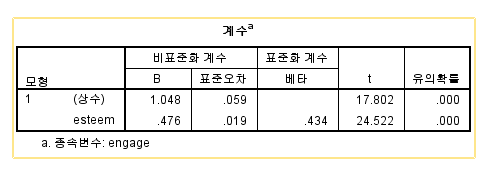
사진 설명을 입력하세요.
단순 회귀식을 표현해보면,
학업열의 = 1.048 + 0.476 * 자아존중감
이 됩니다.
여기서 자아존중감의 평균값을 넣어주면,
1.048 + 0.476*2.99 가 되고, 이 값을 계산하면 놀랍게도..?
1.048+ 1.4234 = 2.47124 로
학업열의 평균과 굉장히 유사한 값이 나오게 됩니다.
구조방정식 모형에 다시 대입하면 이러한 모양이 나옵니다.
즉, '평균 구조'를 포함한 모형에서는
외생변수로 영향을 주는 평균 구조의 계수 값은 '외생변수'의 평균값을 의미하고,
내생변수로 영향을 주는 평균구조의 계수 값은 회귀계수의 절편 값을 의미한다 해석할 수 있습니다.
여기서 주목할 것은 '외생변수'의 평균값입니다.
다시 처음에 보았던 모형으로 돌아가면,
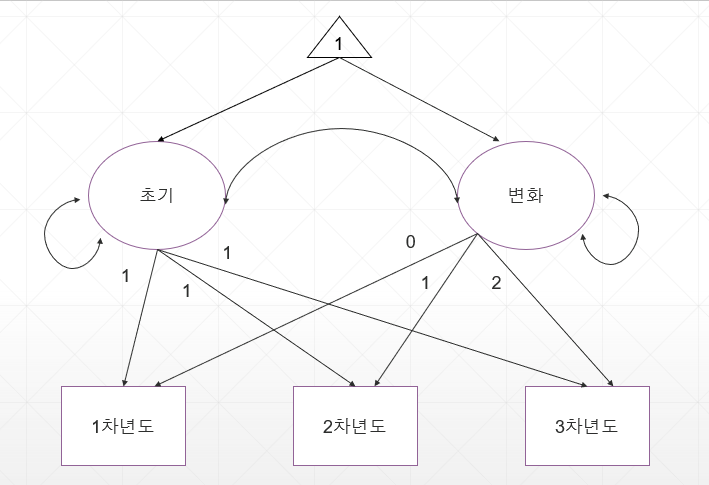
평균 구조가 영향을 주고 있는 '초기'와 '변화'는 외생변수 입니다.
그렇다는 것은 평균 구조의 계수가 나타나면, 이들이 아직은 뭔지 모르겠지만
각각의 '평균값'을 의미하는 것이라는 것을 기억하면 좋을 것 같습니다.
(자세한 설명은 Kline, R. B(2011). Principles and practice of structural equation modeling 여기서.ㅎ)
2. 초기 수준과 변화 수준
이제 초기수준과 변화 수준에 대한 설명을 이어가 볼까요.
잠재성장모형에서 다루는 데이터는 종단 데이터입니다.
예시 모형에서 보였듯이, 1차년도 - 2차년도 - 3차년도 이렇게 시간별로 측정을 하는데
'성장'모형이 듯이
시간이 지날수록 '초기'수준에서 '변화'를 어느 정도 하느냐가 중요합니다.
위 모형에서 '초기' 수준은 1차년도, 2차년도, 3차년도에 '1'값으로 고정을 합니다.
즉, 모든 시점에서 초기 수준은 동일하다고 설정을 해주게 됩니다.
반면 '변화'수준은 시간이 지날수록 0,1,2 점차 커지게 숫자를 설정하였습니다.
말 그대로 시간에 따라 '변화'를 나타내주어야 하니까요.
이렇게 선형으로 변화할 수 있지만, 비선형으로 변화할 수도 있습니다.(이건.. 언젠가 다시 올리는 걸로..ㅋㅎ)
그래서 초기수준과 변화 수준을 합쳤을 때 '총 효과'라고 볼 수 있습니다.
식으로 표현하면,
1차년도 총효과 = 초기수준 * 1 + 변화수준 *0
2차년도 총효과 = 초기수준 *1 + 변화수준 *1
3차년도 총효과 = 초기수준 *1 + 변화수준 *2
이렇게 됩니다.
3. 초기 수준과 변화수준의 공분산
실습으로 넘어가기 앞서 한 가지 더 짚고 넘어갈 것이
초기수준과 변화 수준 사이에공분산이 설정되어 있다는 것이 또 주요 특징인데요
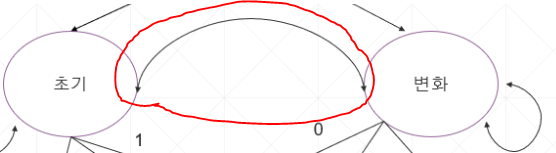
초기 수준과 변화수준이 서로 영향을 주고 받는 것을 설정해 둡니다.
이를 통해 알 수 있는 것은
초기수준과 변화 수준의 공분산 값이 계산되었을 때,
공분산이 양수라면, 초기 수준이 높을수록 변화 수준이 더 크게 나타난다는 것
(초기 수준이 높을수록 변화 수준이 더 작게 나타난다)
공분산이 음수라면, 초기수준이 높을수록 변화수준이 더 작게 나타난다는 것을 의미합니다.
(초기수준이 낮을수록 변화수준이 더 크게 나타난다)
수학 성적을 예로 들면
공분산이 양수로 나왔을 때, 변화 수준도 양수라면
1차년도에 수학 점수가 높으면, 2차년도, 3차년도에 수학점수가 변화가 더 크게 나타날 수 있다는 것
70점 받은 학생과 50점 받은 학생을 비교했을 때,
더 높은 점수를 받은 학생이 이후 시점에 더 크게 크게 점수가 뛰겠죠?
(70 -> 80 -> 90
50 -> 55 -> 60) ... 대충 이런 느낌?
(변화 수준이 음수면, 초기수준이 높을 수록 변화수준이 더 크게 떨어지겠죠?)
반면, 공분산이 음수이고 변화율은 양수라면
1차년도에 수학 점수가 높으면, 이후 시점에 변화가 더 낮게 나타난다
낮으면 더 크게 점수가 뛴다
70 -> 75 -> 80
50 -> 60 -> 70
(여기서 변화 수준이 음수면, 초기수준이 높을수록 변화 수준이 더 작게 낮아지고,
초기수준이 낮을수록 변화수준이 더 크게 낮아지고)
이런 느낌이랄까요..?
실제 분석 결과를 보고 해석하는 게 이해가 더 잘 될 것이라 생각합니다(아마도..?)
이제 이론 그만보고.. R 실습해봅시다..ㅋㅋ
4. 잠재성장모형 분석
데이터는 KCYP2018 1-3차년도 사용합니다.
간단하게(?) 시간에 따른 중학생의 우울이 어떻게 변화하는지,
우울에 어떤 변인이 영향을 주고 있는지 살펴볼까 합니다.
그래서 사용할 변수는 우울, 성별, 학업 무기력입니다.
그럼 일단.. 종단 데이터를 하나로 합쳐야겠네요.
1) 종단 데이터 합치기
변수 만드는 거야 앞에서 많이 했으니까 간단히 캡처로 넘어갑니다ㅋㅋ
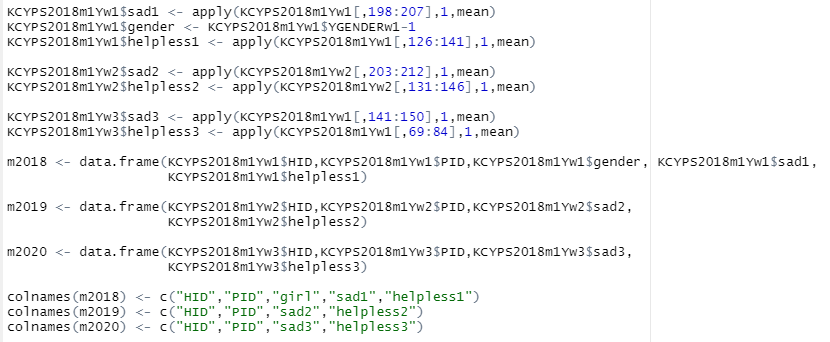
KCYPS2018m1Yw1$sad1 <- apply(KCYPS2018m1Yw1[,198:207],1,mean)
KCYPS2018m1Yw1$gender <- KCYPS2018m1Yw1$YGENDERw1-1
KCYPS2018m1Yw1$helpless1 <- apply(KCYPS2018m1Yw1[,126:141],1,mean)
KCYPS2018m1Yw2$sad2 <- apply(KCYPS2018m1Yw2[,203:212],1,mean)
KCYPS2018m1Yw2$helpless2 <- apply(KCYPS2018m1Yw2[,131:146],1,mean)
KCYPS2018m1Yw3$sad3 <- apply(KCYPS2018m1Yw1[,141:150],1,mean)
KCYPS2018m1Yw3$helpless3 <- apply(KCYPS2018m1Yw1[,69:84],1,mean)
m2018 <- data.frame(KCYPS2018m1Yw1$HID,KCYPS2018m1Yw1$PID,KCYPS2018m1Yw1$gender, KCYPS2018m1Yw1$sad1,
KCYPS2018m1Yw1$helpless1)
m2019 <- data.frame(KCYPS2018m1Yw2$HID,KCYPS2018m1Yw2$PID,KCYPS2018m1Yw2$sad2,
KCYPS2018m1Yw2$helpless2)
m2020 <- data.frame(KCYPS2018m1Yw3$HID,KCYPS2018m1Yw3$PID,KCYPS2018m1Yw3$sad3,
KCYPS2018m1Yw3$helpless3)
colnames(m2018) <- c("HID","PID","girl","sad1","helpless1")
colnames(m2019) <- c("HID","PID","sad2","helpless2")
colnames(m2020) <- c("HID","PID","sad3","helpless3")
결측들은 깔끔하게 싹다 지우는 걸로
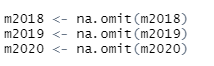
m2018 <- na.omit(m2018)
m2019 <- na.omit(m2019)
m2020 <- na.omit(m2020)
그리고, psych의 describe으로 기술통계 살짝 확인해주고..
library(psych)
describe(m2018)
describe(m2019)
describe(m2020)



HID, PID는 학생들에게 부여한 개인 ID입니다. 그래서 무시해도 괜찮고,
성별은 웬만하면 바뀌지 않을 테니, 1차년도에만 넣어주었고
나머지에 각각 우울, 학업 무기력을 만들어서 넣어주었습니다.
이 3개의 데이터를 통합하기 위해 merge 함수를 사용합니다.
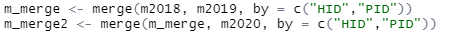
merege(데이터프레임1, 데이터프레임2, by = 기준변수)
이런 구조인데, 이 데이터는 기준변수를 두 개나 활용해서, 위와 같이 설정을 해주어야 잘 묶입니다.
그래서 잘 묶였다면,
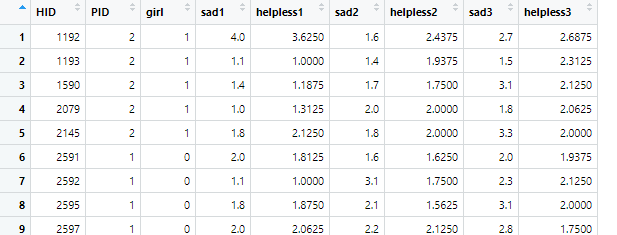
이런 식으로 기준 변수(HID, PID)에 각 변수들이 옆에 붙게 됩니다.
이러면 진짜 분석 준비 끝입니다.
2) 잠재성장모형 분석하기
앞서 사용했던, lavaan 패키지 사용하고요, semplot 패키지까지 덤으로 있으면 좋을 것 같기도 합니다
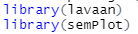
사진 설명을 입력하세요.
처음에는 무조건 모형으로 분석을 해볼게요.
모델은 다음과 같이 설정합니다.
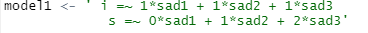
i는 초기 수준
s는 변화 수준을 의미하고,
초기 수준에는 1씩 곱해주고, 변화 수준에는 0,1,2를 곱해줍니다.
그리고 growth를 사용해서 잠재성장모형을 분석하고
summary를 확인해주면 됩니다
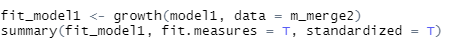
먼저 모델 핏을 보면...

와... 최악이네요ㅋㅋㅋ
만약 이런 모델핏이면.. 당장 뭐 때려치워야 하지만..
연습이니까.. 넘어갑시다...ㅋㅋㅋ
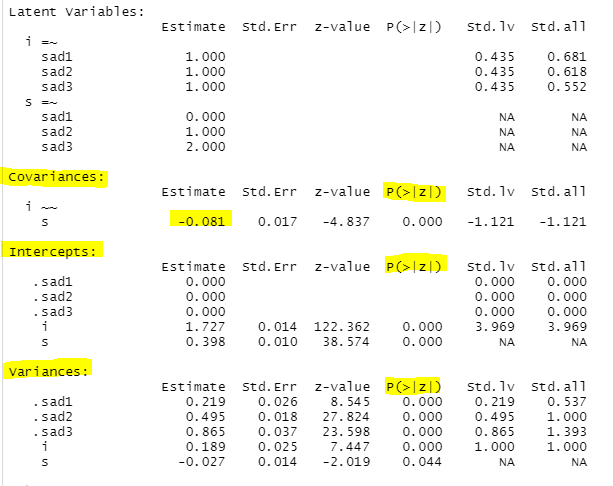
Covariance 공분산이 음수이고, 통계적으로 유의하네요
Intercepts 초기 수준 1.727, 변화 수준 0.398 모두 통계적으로 유의합니다.
Variances 분산도 초기 수준, 변화 수준 통계적으로 유의하게 나왔습니다.
이를 종합해서 서술한다면,
중1의 우울은 평균 1.727로 나타났고, 중학교 시기 동안 우울의 평균 변화율은 0.398로 우울이 점차 증가하는 것으로 나타났다.
초기 수준과 변화수준의 공분산은 음수로, 우울의 초기치가 높을수록 변화율이 낮은 것으로 나타났다.
우울의 초기수준과 변화수준의 분산이 모두 통계적으로 유의하므로, 초기수준과 변화 수준에서 개인차가 있는 것으로 나타났다.
3) 조건 추가한 잠재성장모형
여기에 이제 아까 변수로 만들어둔 성별(여학생 더미), 학업 무기력을 사용해보려 합니다.
생각해보니, 학업무기력을 매 시점마다 만들어두었는데
1차년도 값 밖에 쓸 수 없었단 사실.. 휴..
조건에 보통 1차년도 값을 넣는 것 같습니다.
하긴 2차, 3차 값이 어떻게 1차에 영향을 주나..
아무튼..
모델은 두 줄 정도 추가됩니다.
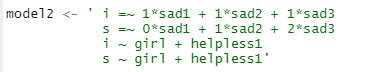
초기, 변화 수준 밑에다
i ~ 조건변수 1 + 조건변수 2
s ~ 조건변수 1+ 조건변수 2
이걸 추가해줍니다.
마찬가지로 분석을 돌리면,
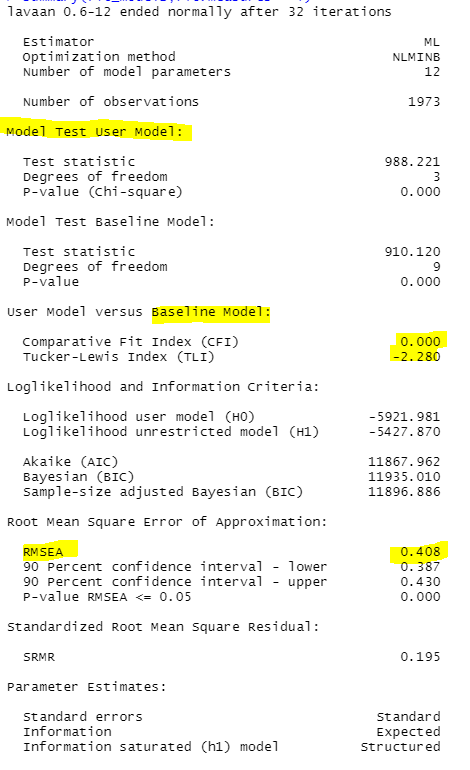
사진 설명을 입력하세요.
모델핏... 휴..ㅋㅋㅋ
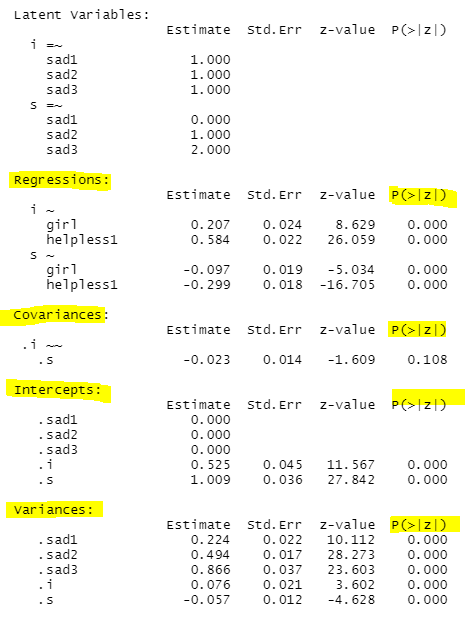
Regressions : 모두 통계적으로 유의하고,
남학생에 비해 여학생인 경우 우울 초기 수준이. 207 더 높고
학업 무기력 초기 수준은. 584로 나타났습니다.
학업 무기력이 높을수록 우울이 높은 것으로 나타났습니다.
남학생에 비해 여학생인 경우 우울 변화 수준이. 097 더 낮고(음수니까)
학업 무기력 변화 수준이 -.299로 나타났습니다.
학업 무기력이 높을수록 우울이 더 크게 낮아지는 것으로 나타났습니다.
(뭐 이런 결과가 나오나 싶지만.. 통계가 이렇게 나오네요..?ㅋㅋㅋ
모델핏이 이상하니까 어차피 쓰지 못하는 거지만 아무튼..)
intercept: 초기 수준. 525, 변화 수준 1.009로 나타났고 통계적으로 유의합니다.
covariance: 공분산이 통계적으로 유의하지 않는 것으로 나타났습니다.
variance: 초기 수준, 변화 수준 모두 통계적으로 유의하므로 개인차가 존재하는 것으로 보입니다.
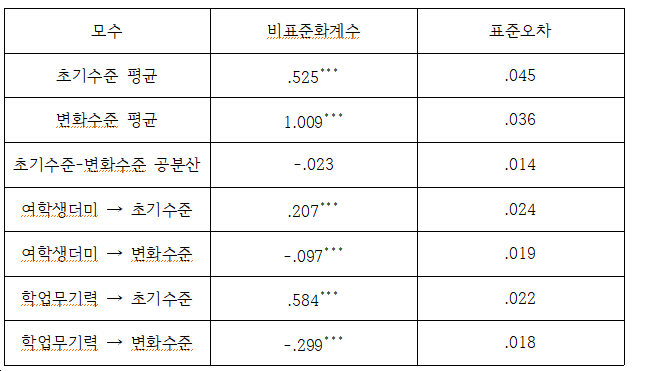
이렇게 결괏값들을 정리하면,
그림도 같이 제시하면 좋겠죠.
diagram <- semPlot::semPaths(fit_model1,
whatLabels = "est", intercepts = F, style = 'lisrel',
nCharNodes = 0,
nCharEdges = 0,
curveAdjacent = T, title = T, layout = "tree2", curvePivot = T)
semPlot으로 그림을 그릴 수 있긴 한데
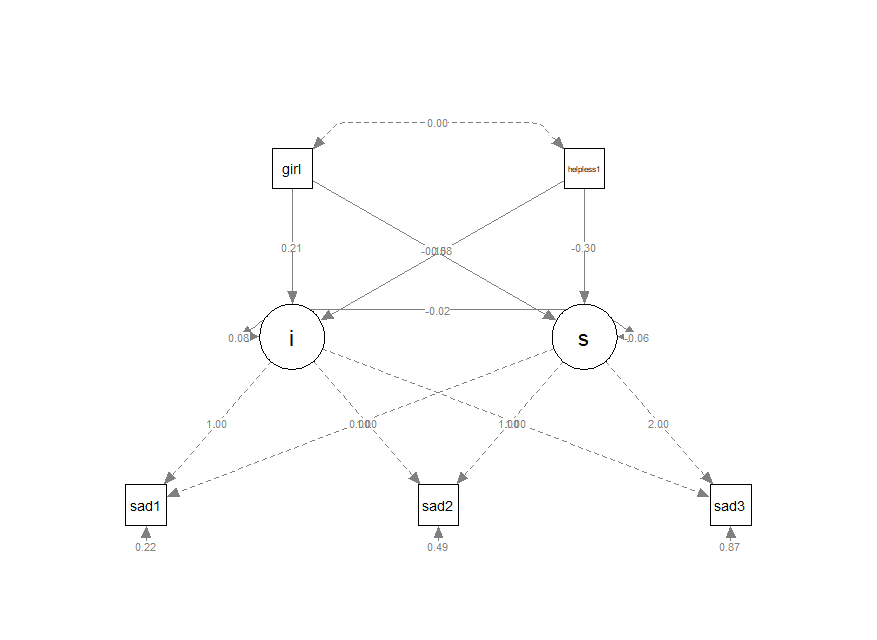
마음에 안 듭니다...ㅋㅋㅋ
근데 논문 몇 개 찾아보면... 모형만 제시하고
그림은 잘 안 보여주는 것 같아서..
저도 패스...ㅎㅎㅎ
결과만 잘 정리해서 보여줍시다..!
'교육통계 > Rstudio' 카테고리의 다른 글
| 교육통계 R랑가몰라 2. 기초통계 - 3) 다중회귀분석1 (0) | 2022.11.03 |
|---|---|
| 교육통계 R랑가몰라 9. 구조방정식(SEM) 5) 자기회귀교차지연모형 (0) | 2022.11.03 |
| 교육통계 R랑가몰라 9. 구조방정식(SEM) 3) 경로모형 (0) | 2022.11.03 |
| 교육통계 R랑가몰라 9. 구조방정식(SEM) 2) 모형검증 (0) | 2022.11.03 |
| 교육통계 R랑가몰라 9. 구조방정식(SEM) 1) 요인분석(확인적요인분석) (0) | 2022.11.03 |