1.상호작용?
A, B 따로 따로 보는 게 아니라
사실 같은 영향안에 있는 것이니까
서로 상호작용이 있는 거 아니냐?
원래있던 기득권 세력인
주효과 A, B와 함께
상호작용효과 A*B도 고려해야 하는 것 아닌가 하는 생각은 또 누가 시작했을 까

상호작용 효과가 있다면,
그 평균의 차이가 주효과(A, B)에 의한 것이 아니라
서로 영향을 주고 받고 있어서 주효과+상호작용 효과로 봐야 되는 것 아닌가?
라고 누가 시작했다
상호작용 효과를 확인하기 위해서는 그래프과 효과적이긴 한데
상호작용이 없는 경우, 두 직선이 평행 또는 일치된 상태를 보인다
x축에 집단 변수 둘 중 1개, Y축은 종속변수
x축은 해당 수준에 따른 값을 표기해준다
아래 그림에선 X1, X2 모두 2개의 수준만 가지고 있다고 했을 때
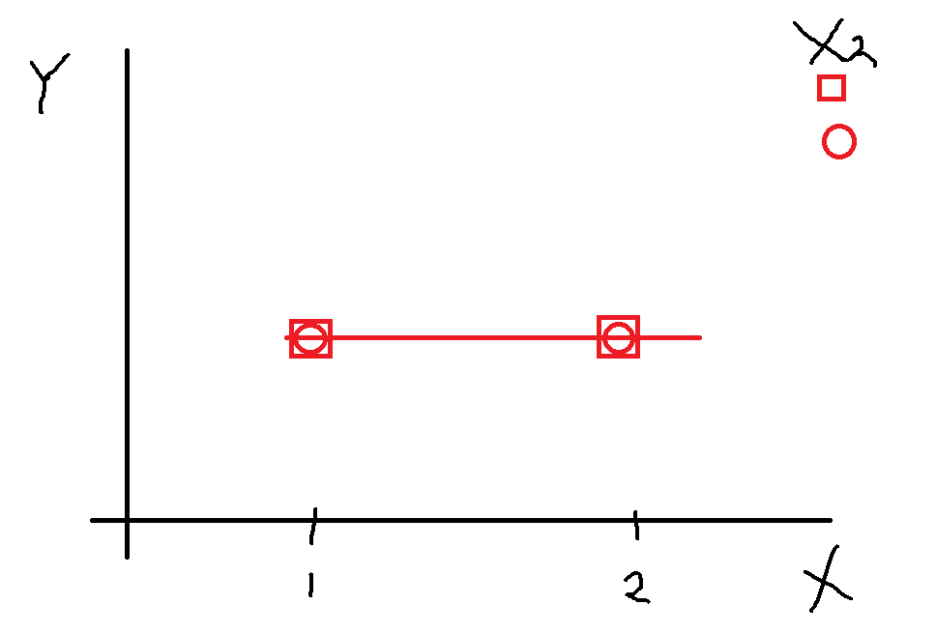
이렇게 네모와 동그라미가 일차하는 경우
어떤 수준에서던 평균이 동일한 것임을 보이는 것이기 때문에
상호작용은 물론 주효과도 없는 모습이다
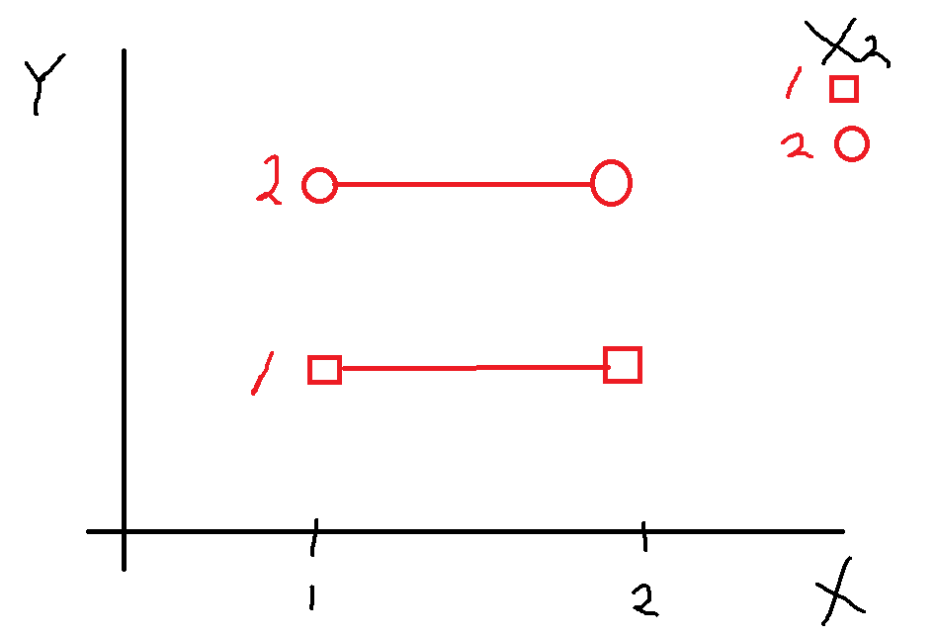
이 그래프는 X1에 대한 효과는 없고
X2에 대한 효과만 존재하는 것으로 볼 수 있다
X가 어떤 수준이든 Y값이 동일하나,
X2의 수준에 따라 Y값이 다름을 보이고 있다
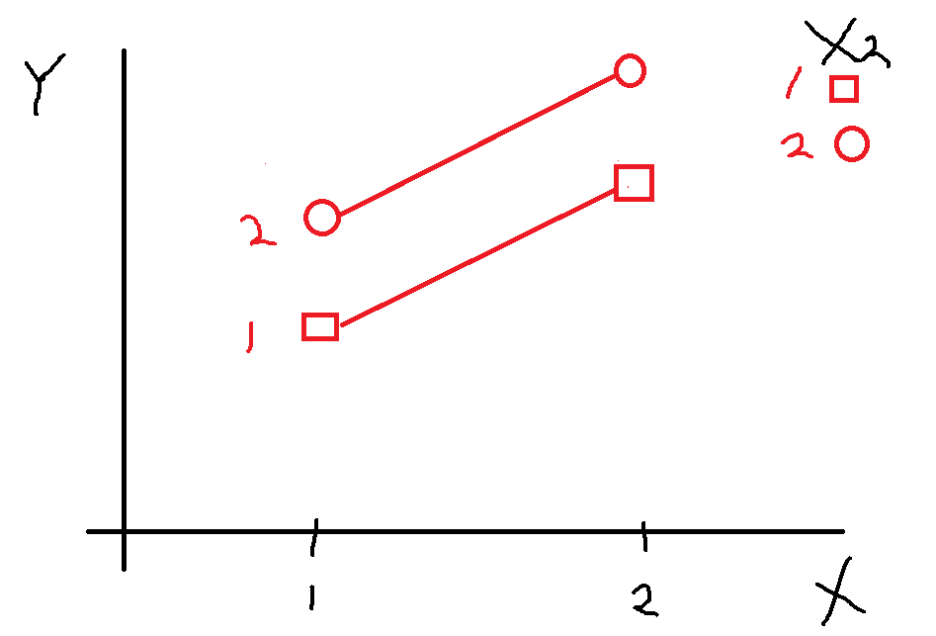
이렇게 평행하게 상승 또는 감소할 때도 마찬가지로
상호작용효과는 없는 것
그러면 상호작용효과가 있다면?
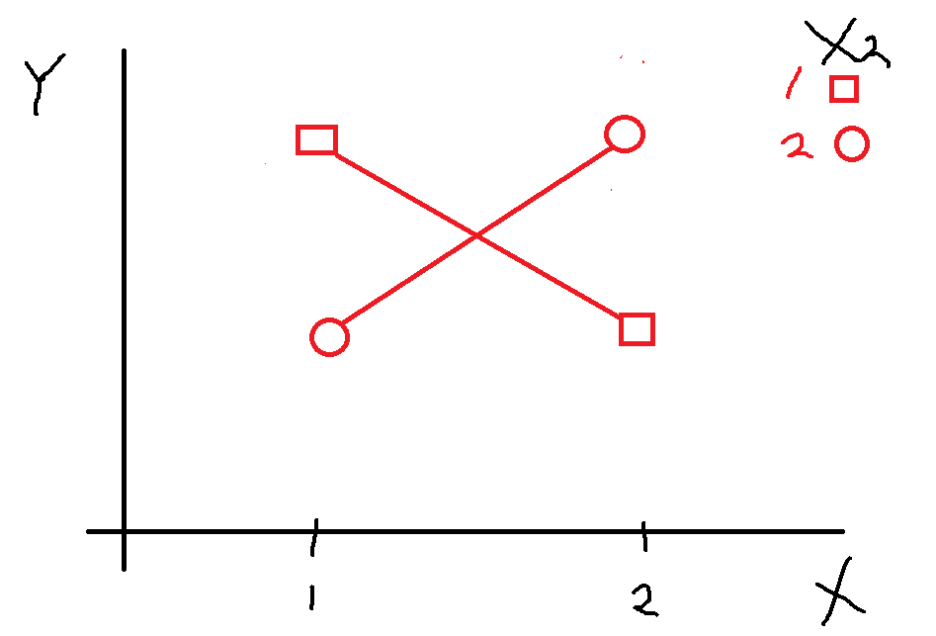
이 그림은 상호작용 효과는 존재하고
주효과는 없는 것을 의미한다
X1 수준에 따라 X2 평균값이 반대로 뒤바뀌기 때문에
상호작용효과만 존재하고
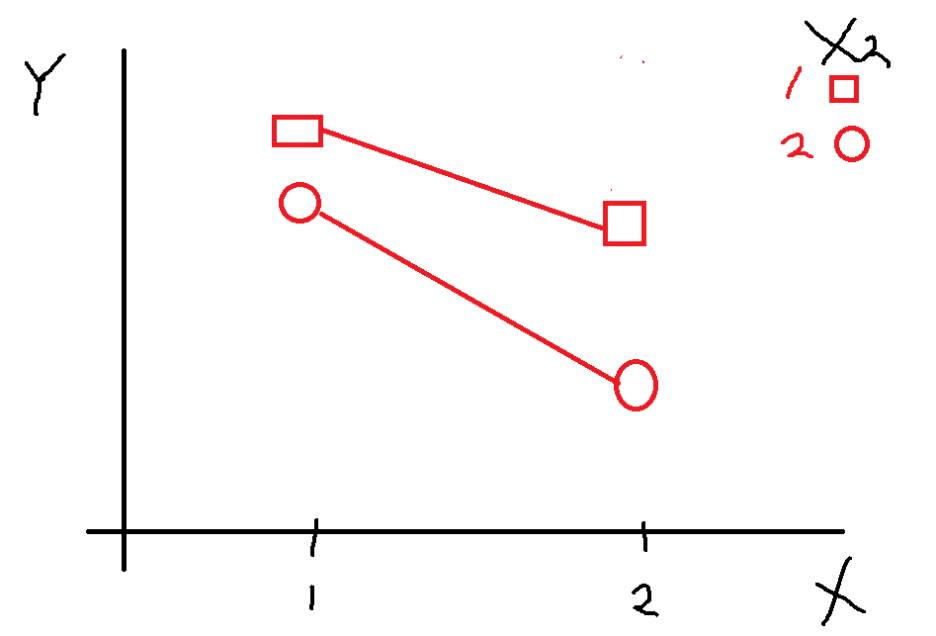
평행하지 않고
기울기가 변화하면서 언제 어디선가 만날 것 같은
모양을 보이면 상호작용이 있음을 보일 수 있다
2.아오 수식시치
그럼 상호작용 분석은 어케?
분산분석표가 해결해줄꺼야
그걸 위한 또 수식..
시작을 일단 A*B로 간다
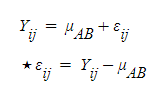
이렇게 되면, 각 개개인의 값은
A, B 그룹의 곱한 값으로 정의하고,
오차는 그 곱의 값을 뺀 것으로 보게 된다
그 다음 이제 또
분산분석스럽게 수식을 바꿔주기 위해
주작을 시작해보자..
좌우에 먼저 전체 평균 값을 빼주고
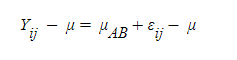
넣어도 수식상 아무 문제 없는
수식을 우측에 넣어준다

그러고 이제 보기 좋게 정리해주면,
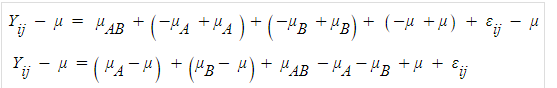
그리고 표본평균값으로 대체해서 묶어주면
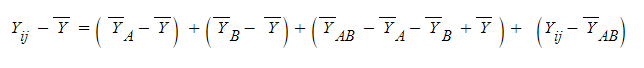
A집단 편차, B집단 편차, 뭔지 모를 복잡한 편차, 오차항
으로 정리가 된다
이거를 이제 편차 합으로 다시 바꿔주면,
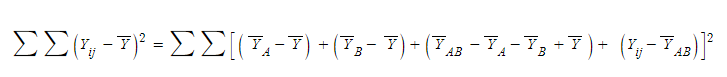
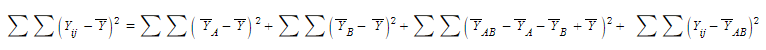
편차제곱 합= A 집단 편차제곱합+B집단 편차제곱합+ A* B집단 상호작용 제곱합+집단내 제곱합
저 괴상한 수식을
왜 A*B 상호작용항이라 할 수 있는가?
*이 아래의 수식은 진짜 뇌피셜이라 정확하지 않을 수 있음
**그래도 이해한 방식을 공유하기 위해 일단 어거지로 한 번 써 봄 ㅋㅋ
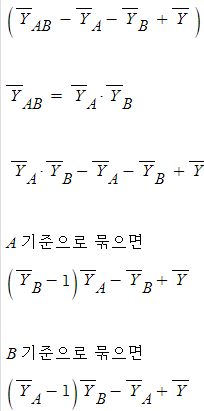
보기 좀 어지럽지만
간단히 쓰면
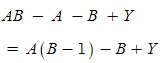
A와 B의 평균간 서로 영향을 주고 받고 있는 구조일 수 있다고
볼 수 있지 않나..? 아몰랑
어찌되었건,
분산분석표로 정리하면
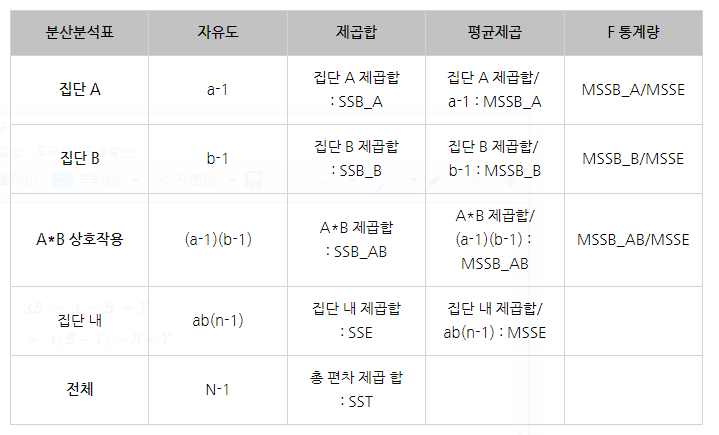
상호작용항을 보면
저번 이원분산분석에서 집단내 자유도 오차와 같은 것을 볼 수 있다
근데 집단 내 자유도는 n-1이 추가되었다
이건 또 뭐야
사실은 상호작용항을 넣을려면,
데이터구조가 기존 분석틀과 살짝 다르다,
'반복측정'이 되어야만 상호작용 효과를 볼 수 있는데
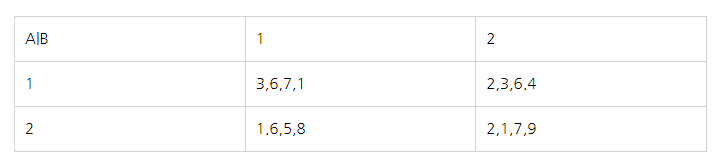
이런 식으로 되어있을 때,
통계적으로 오차 계산, 모수 추정에 문제가 안 생긴다나 뭐라나..
그래서 집단 내 오차에 들어가는 n-1에서의 n = 반복 수 라고 보면 된다
1*1 셀안에 있는 숫자의 개수인 n = 4 가 된다
3. 그래서 분석은?
교사성취압력에 긍정적 수업분위기, 교사열의 수준별로 차이가 있을 것 같다는 생각이 갑자기 들었고
이왕 하는김에 두 가지 요인(긍정적 수업분위기, 교사열의)간 상호작용 효과가 있지 않을까도 같이 생각해보자
연속형 변수이기 때문에,
범주형 변수로 코딩을 일단 해준다음
data %>% mutate(긍정적수업분위기4수준 = case_when(긍정적수업분위기 >= 1 & 긍정적수업분위기 < 2 ~ '1',
긍정적수업분위기 >= 2 & 긍정적수업분위기 < 3 ~ '2',
긍정적수업분위기 >= 3 & 긍정적수업분위기 < 4 ~ '3',
긍정적수업분위기 >= 4 & 긍정적수업분위기 <= 5 ~ '4',
TRUE ~ NA),
교사열의4수준 = case_when(교사열의 >= 1 & 교사열의 < 2 ~ '1',
교사열의 >= 2 & 교사열의 < 3 ~ '2',
교사열의 >= 3 & 교사열의 < 4 ~ '3',
교사열의 >= 4 & 교사열의 <= 5 ~ '4',
TRUE ~ NA)) %>%
select(교사성취압력, 긍정적수업분위기4수준, 교사열의4수준) -> test
두 변수를 펙터로 변환해준다
test$긍정적수업분위기4수준 <- as.factor(test$긍정적수업분위기4수준)
test$교사열의4수준 <- as.factor(test$교사열의4수준)
분석을 돌려보면,
model_aov_inter <- aov(교사성취압력 ~ 긍정적수업분위기4수준*교사열의4수준, data = test)
상호작용항은 *으로 연결해주면 된다
summary(model_aov_inter)
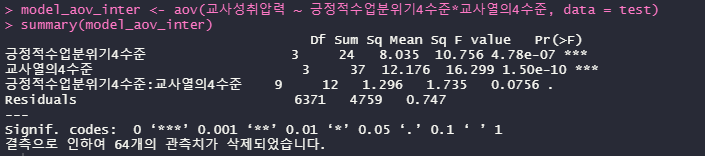
아...상호작용항이 아슬아슬하게 유의하지 않는 것으로 나와버렸네..
그래도 아쉬우니 그래프는 그려보았다
with(data, interaction.plot(1요인, 2요인, 종속변수))의 꼴을 가지고 있는 것을 적용해서 그려보면
with(test, interaction.plot(긍정적수업분위기4수준, 교사열의4수준, 교사성취압력))
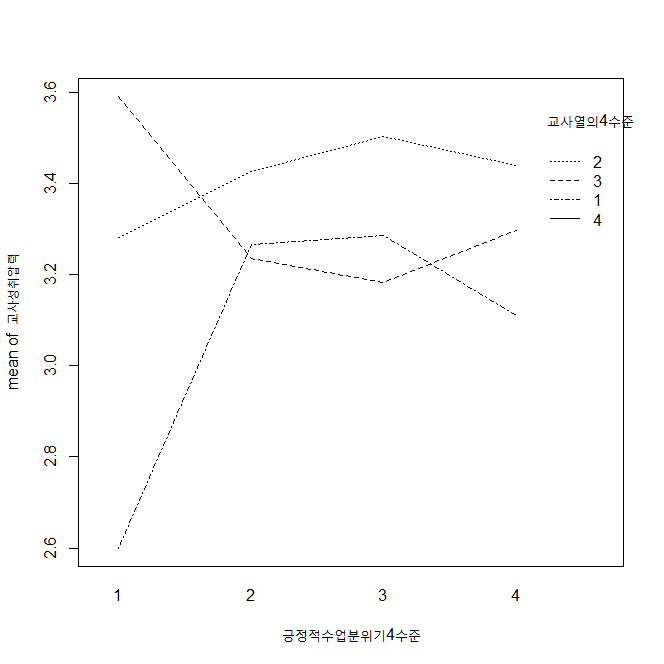
교사열의 4수준이 의미없나 보다.. 곡선이 없어졌네..ㅋㅋ
잘라서 보면,
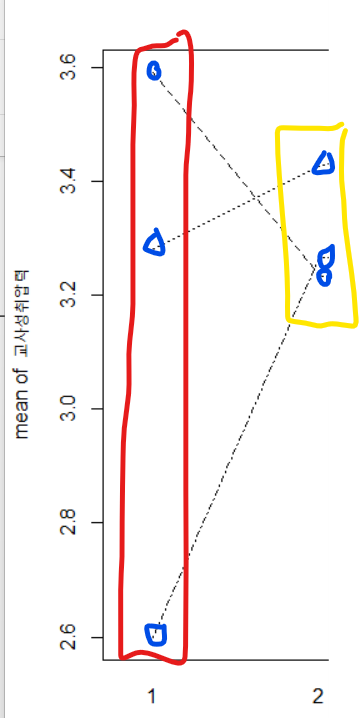
긍정적 수업 분위기 수준이 1일 때. 교사열의 수준에 따라
교사 성취압력 평균의 차이가 굉장히 크게 나타나는데
긍정적 수업 분위기 수준이 2일 때는 교사열의 평균이 모이게 되면서,
기울기들이 다소 정신 없이 왔다갔다 하는 패턴을 보인다
물론, anova 테이블에서는 상호작용 효과가 없는 것으로 보이지만,
만약, 유의한 결과를 가져왔다면
연구자 관심 변수에 따라 해석을 이어가면 될 것 같다.
4. SPSS로 한다면?
분석 -> 일반선형모형 -> 일변량
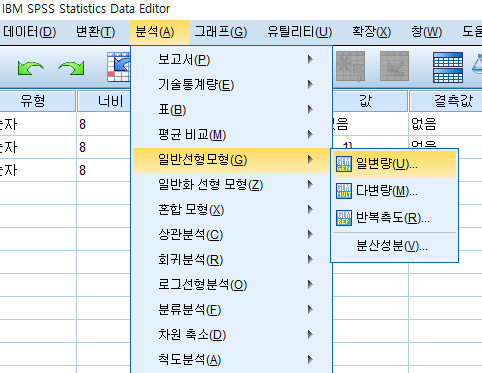
종속변수에 넣고
고정요인(또는 변량요인)에 각 변수 넣고
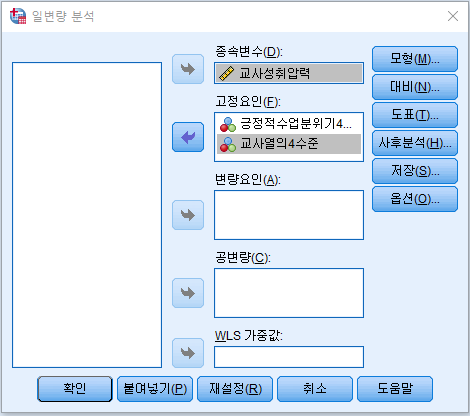
그래프도 보고 싶으니 도표 누르고
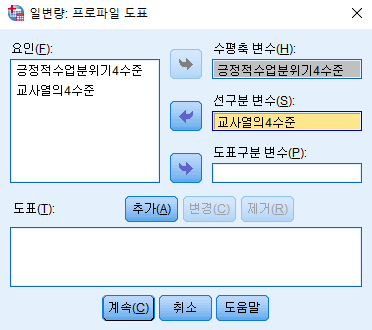
도표에 수평축, 선구분에 먼저 넣고
그다음 추가 클릭
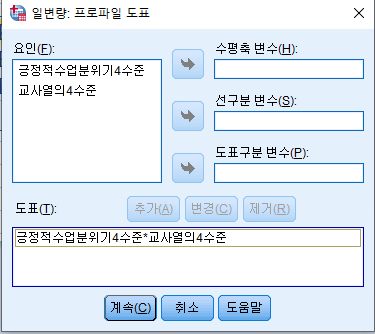
그 다음 계속
사후분석까지 걍 눌러부르
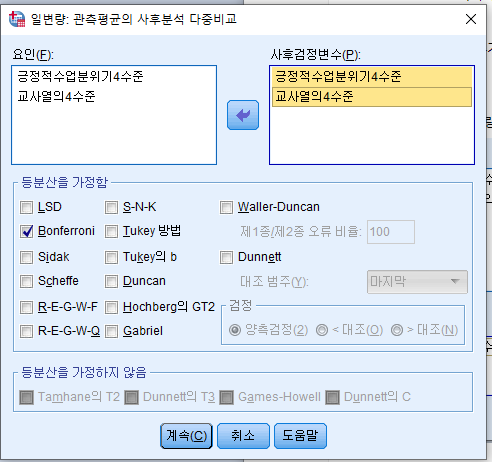
이카면 끝?
분석 결과 확인~
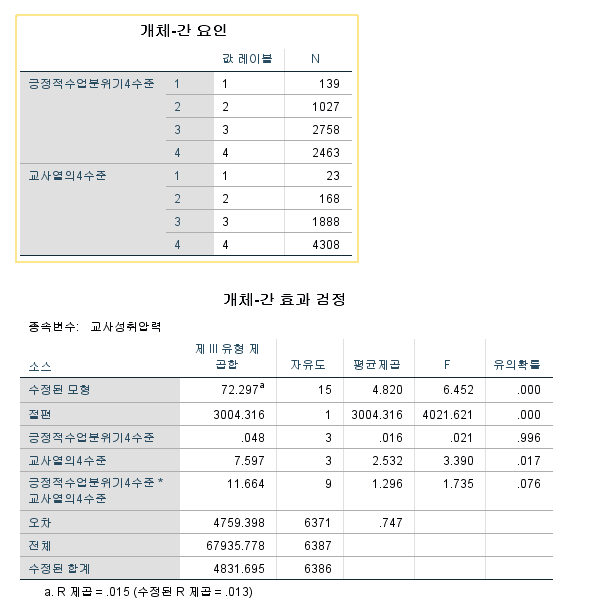
유의도 확인해주고
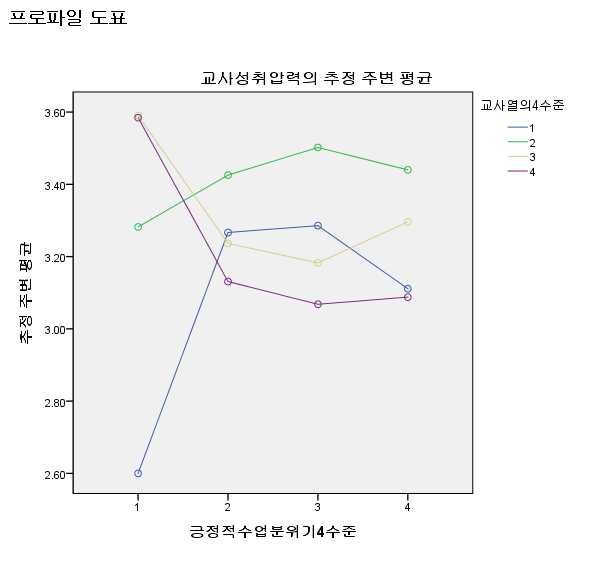
오 이건 그래프 다 그려주네
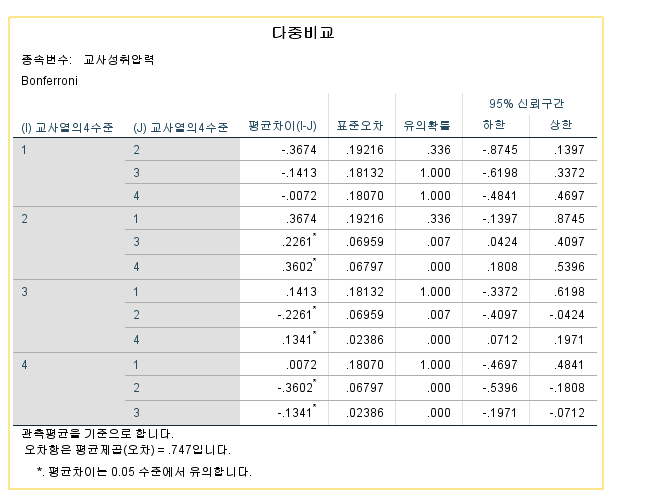
유의한 결과에 맞춰서 사후분석까지 하면
진짜진짜 끝?
'교육통계 > STATA' 카테고리의 다른 글
| 분산분석 4. 이원분산분석 (0) | 2023.09.04 |
|---|---|
| 분산분석 3. 일원분산분석 (0) | 2023.09.04 |
| STATA - 5.다중회귀 (0) | 2023.09.04 |
| STATA - 4.상관 & 단순회귀 (0) | 2023.09.04 |
| STATA- 3. 기술통계 (0) | 2023.09.04 |