일원분산분석에서
요인, 집단을 구부하는 변수 하나만 넣고 분석을 한 건데
두 개 넣고 싶으면 어쩌나
했을 때 쓰는 방법이 이원분산분석
가령, 앞서 우울을 지역규모로만 구별해서 분석을 했는데
학교 성별유형(남녀공학, 남학교, 여학교)에 따라서도 약간 차이있지 않을까
라는 쓸데없는 생각이 든다면
그 때 쓸 수 있다.
아니 근데 두 개면 일원분산분석 두 번 하면 되는 거 아니냐고 할 수 있는데
그걸 언제 하나 하나 돌리고 있노..
보다는 t-test 에서 다중검정의 문제가 있을 수 있으니
그냥 한 큐에 하자고..
1.일단 먼저 고정효과모형
수식을 살펴보자

A집단의 평균과 B집단의 평균과 함께 오차항으로 구성되어 있고
이걸 다시 풀어쓰면


세상 끔찍하지만
한 번 만 더 분산분석스럽게 정리하면

---
중간 과정까진 도저히
마음이 꺾여서 못하겠다
아무튼 결론은

이 구조를 통해 분산분석표를 만들어보면
집단 A는 a 만큼 있고
집단 B는 b 만큼 있다고 했을 때,

집단 A 자유도나 집단 B 자유도는 일원분사분석이랑 마찬가진데
왜 집단 내는 (a-1)+(b-1)이 아니고
(a-1)*(b-1)이냐
...
이원분산분석에 쓰이는 데이터 구조 때문으로 추정되는데
예를 들면

N=12 라고 했을 때
이런식으로 구조화 되어 있다
집단 A 자유도 빠지고, 3
집단 B 자유도 빠지면, 2
이 둘을 곱한게 남아있는 부분(집단내) 자유도가 되는데
N-1 = (a-1)+(b-1)+(a-1)*(b-1)
11 = 3+2+3*2
이렇게 나온다
'자유도'라서 이런 개념으로 되는 것 같은데
뭐.. 맞지 않나 싶다 하고 또 넘어가자
(마음이 많이 꺾였다)
어찌됐든 분산분석표에 의해
집단 A 기준으로 F통계량이 유의하면, 집단 A 수준별 평균에 차이가 있다
집단 B 기준으로 F통계량이 유의하면, 집단 B 수준별 평균에 차이가 있다
하고 사후분석 마찬가지로 진행하면 된다
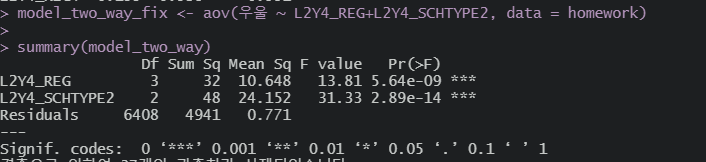
오 지역규모나 설립유형이나 모두 통과됐네
그럼 사후분석 해주면 되겄지?
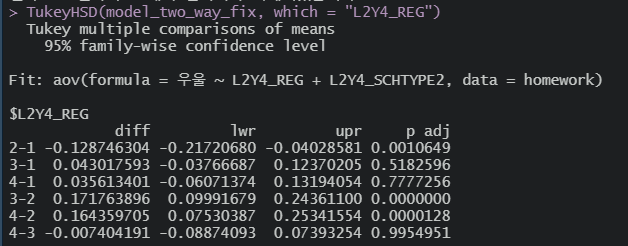
유의한 차이를 보인 건
'2-1', '3-2', '4-2' 정도
중소도시에 비해 읍면지역이 평균 우울이 낮고
중소도시에 비해 대도시가 평균 우울이 높고
중소도시에 비해 특별시 평균 우울이 높네(저런..)
2. 무선효과
무선효과도 마찬가지
F검정 분산분석표 그대로 사용하면 되고
주된 관심은 분산이 0이냐 아니냐 이지
수준별로 평균이 어쩌구에는 관심이 없다
바로 분석 넘어가면,

각 분산 성분에 따라서 ICC 계산해서 이야기하면 되고,
코드에서 바뀐 것은 무선효과 +(1|L2Y4_REG) +(1|L2Y4_SCHTYPE2)
두 개 써준 것 정도?
3. 이 두 개를 합친게 혼합모형
고정효과, 무선효과만 해서 노잼이면
이 두 개 섞어서 추정해도 된다
그럼 혼합모형
똑같은 분산분석표 여전히 활용하되,
연구자가 설정한 모형에 따라 사후분석 또는 ICC 계산 하면 된다

lmer함수에 고정효과는 그대로 써주고, 무선효과는 +(1|변수)로 추정하면 확인 가능하다
뒤에 붙는 해석은 마찬가지로 진행하면 끝~!
'교육통계 > STATA' 카테고리의 다른 글
| 분산분석 5. 상호작용 (0) | 2023.09.04 |
|---|---|
| 분산분석 3. 일원분산분석 (0) | 2023.09.04 |
| STATA - 5.다중회귀 (0) | 2023.09.04 |
| STATA - 4.상관 & 단순회귀 (0) | 2023.09.04 |
| STATA- 3. 기술통계 (0) | 2023.09.04 |