분산과 평균의 관련성에 대해 간략히 살펴보았고,
그럼 통계적으로 어떻게 검정할 것인가?
1. 분포가 뭐노 먹는건가?
각 통계량들은 각각 사용되는 확률분포로 부터 검정을 실시한다
이왕 시작하는거 처음으로 돌아가자
일단 '모평균'에 대한 통계적 추론을 한다고 했을 때,
정규분포로 시작해서 t분포로 이어지는 흐름은
아래 글에 열심히 정리한 기억이 갑자기 생각났다
https://blog.naver.com/tmalqr/223095864877
그럼 분산은 어떤 분포를 따르는 가? 라고 했을 때
t분포를 제곱해서 모두 합친 카이제곱분포를 따르게 된다
t분포를 제곱해서 합쳤기 때문에
0부터 시작하는 괴상한 모양의 분포가 만들어진다
표본분포에서의 자유도는 n-1

사진 설명을 입력하세요.
*카이제곱분포 그리는 R 코드는 아래 참조
library(ggplot2)
df <- 1
df2 <- 2
df3 <- 3
df4 <- 4
df5 <- 5
x <- seq(0, 20, by = 0.1)
density <- dchisq(x, df)
density2 <- dchisq(x, df2)
density3 <- dchisq(x, df3)
density4 <- dchisq(x, df4)
density5 <- dchisq(x, df5)
df <- data.frame(x, density, density2, density3, density4, density5)
ggplot(df, aes(x)) +
geom_line(aes(y = density, color = "df = 1")) +
geom_line(aes(y = density2, color = "df = 2")) +
geom_line(aes(y = density3, color = "df = 3")) +
geom_line(aes(y = density4, color = "df = 4")) +
geom_line(aes(y = density5, color = "df = 5")) +
labs(title = "Chi-squared Distribution", x = "x", y = "Density") +
scale_color_manual(values = c("df = 1" = "blue",
"df = 2" = "red" ,
"df = 3" = "green",
"df = 4" = "yellow" ,
"df = 5" = "purple")) +
theme_minimal()
이 분포를 활용해서 표본분산 통계적 추론을 검정한다
2. 아니 그래서 분산분석 검정 어케하냐고
그러면 이제, 두 집단간 분산은 어떻게 검정하는가라고 했을 때,

이 검정을 위해 '비율'을 활용한다
만약, A집단의 분산과 B 집단의 분산이 같다면 '1' 이 될 것이고
그렇지 않으면 '1'보다 크게 될 것이다
다시 표현하면

이렇게 되었을 때, 이 분산의 비율은 F분포를 따르게 된다

F분포를 보면 자유도를 2개 취하는데 그 이유는
분자, 분모가 각각 카이제곱분포를 따르고 있기 때문이고,
그 분포를 결합한 것이 F분포가 되기 때문이다
분자에서의 자유도
분모에서의 자유도
그래서 F분포가 이렇게 써있더라

이렇게 총 2개의 자유도를 취하는 또 하나의 괴상한 분포가 있다는 것이라나 뭐라나
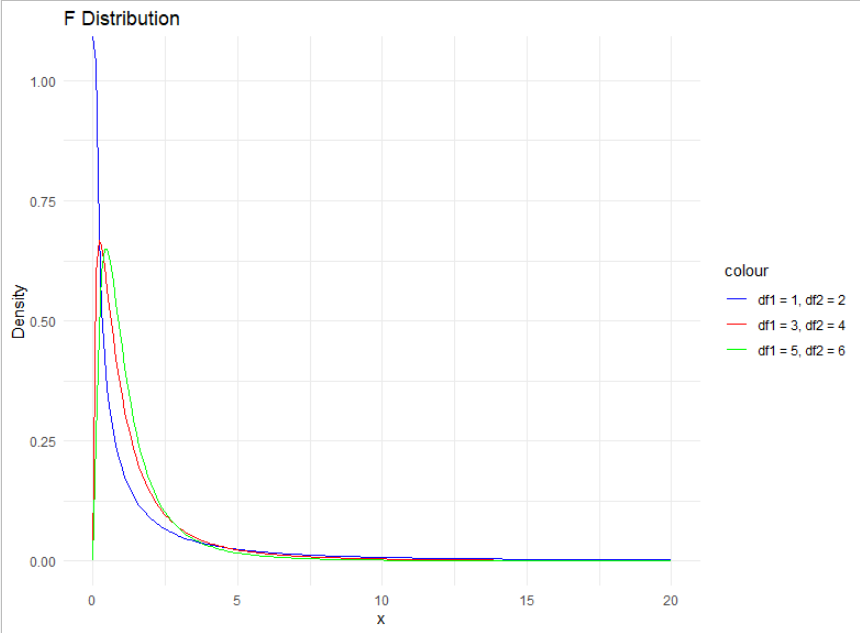
*F분포 R코드
x <- seq(0, 20, by = 0.1)
density_df_1_2 <- df(x, df1 = 1, df2 = 2)
density_df_3_4 <- df(x, df1 = 3, df2 = 4)
density_df_5_6 <- df(x, df1 = 5, df2 = 6)
f_df <- data.frame(x, density_df_1_2, density_df_3_4, density_df_5_6)
ggplot(f_df, aes(x)) +
geom_line(aes(y = density_df_1_2, color = "df1 = 1, df2 = 2")) +
geom_line(aes(y = density_df_3_4, color = "df1 = 3, df2 = 4")) +
geom_line(aes(y = density_df_5_6, color = "df1 = 5, df2 = 6")) +
labs(title = "F Distribution", x = "x", y = "Density") +
scale_color_manual(values = c("df1 = 1, df2 = 2" = "blue",
"df1 = 3, df2 = 4" = "red",
"df1 = 5, df2 = 6" = "green")) +
theme_minimal()
그래서 위, 아래가 분산의 형태를 띄고 있을 때의 검정은
F분포를 활용한다
3. 그래서 이거 얘기하려고 여태 빌드업?
다시 t검정으로 돌아가보면,

여기서 이제 t검정만 하면 다중검정의 오류가 발생하니,
이걸 제곱해준다
제곱하면 머선일이 일어나냐
수식과 함께 알아보자ㅋㅋ

일단 여기까지는
중등 교육과정의 기억이 아직 남아있다면
충분히 따라가는데 문제없을 수도..?
그 다음은 이제 그냥 '치환' 바꿔치기만 해주면 된다
먼저 바꿔치기할 부분은 분자인
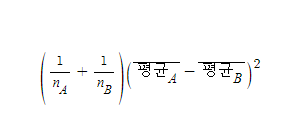
이거슨
A집단과 B집단의 전체 평균을 정리하면,
다음과 같이 정리된다
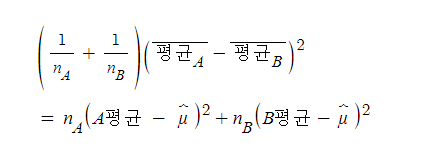
이 때

이렇게 '분자'에 쌓여있는 분산을 정리할 수 있게 된다
그 다음 분모에 있던
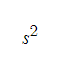
이 친구는 합동표본분산으로 불리면서
이걸 전개하면

가 된다
다시 이렇게 정리한 분자와 분모를 합쳐보자

이렇게 또 해괴망측한 수식이 나타났다
왜 이렇게 기를 쓰고 전개를 했냐하면
다시 이 수식을 보면 분자도 분수의 형태로 표현할 수 있다

이 기괴한 식을 다시 찬찬히 살펴보면

사진 설명을 입력하세요.
위 아래 모두 '분산'의 구조를 가지고 있으면서,
자유도는 각각의 '분모'를 가지는 형태로 본다
분자는 왜 자유도가 1이냐
전체평균 = (A평균 + B평균) / 2 이니까
1개만 고정되면, 나머지 1개는 뭔 값이 오든 상관이 없으니까
분모의 자유도는 nA+nB-2냐
전체 분산을 구하는 과정에서 고정된 것은 A평균, B평균 2개니까
다시 바꿔서 설명하면,
분자에서의 자유도는 '집단수 -1'
분모에서의 자유도는 '전체사례수 - 집단수' 가 된다
만약 집단이 3개 이상인 경우에는 어떻게 식이 바뀌는가하면

어우 더 뭔소린가 싶은데 다시 여기서 줄이면

로 요약이 된다
분자는 왜 집단 간 분산이냐
'전체평균'을 중심으로 각 집단의 평균이 어느 정도 떨어져 있는 가를 계산했기 때문이고
분모는 왜 집단 내 분산이냐
'각 집단별 평균'을 중심으로 개인의 값들이 어느 정도 떨어져 있는지 보여주고 있기 때문이다
이 분산비를 활용해서
F분포를 따르는 F검정을 실시한다
어우 끔찍
4. 마무리
F검정의 결론이 어떻게 되느냐

F=1 이거나, F가 1보다 작으면 문제가 있다
왜냐?
집단 간 분산 보다 집단 내 분산이 더 크다는 것을 의미
즉, 집단별로 분리해도 별 차이 없는데
굳이 굳이 집단을 왜 나눔?
라는 것을 의미한다
차이가 유의미하다면, 집단별로 보는게 의미 있을 텐데
이게 무슨 의미가 있니 라는 멘트로 끝나게 된다
이때 집단 간 분산이 발생한 이유는
원래 결과변수 모집단에서 표본집단을 만들 때 생긴
표집오차에 의한 것이다~
라고 더 그럴듯 한 결론을 내릴 수 있다
반대로 F가 1보다 크면서 유의수준을 넘기면
집단 간 차이가 유의미하다 하고
다음 단계로 넘어갈 수 있게 된다
(예를 들면 사후분석?)
*여기서 한 가지 짚고 넘어가면,
분모를 형성하는 집단 내 분산 계산할 때
가정은, 각 집단이 동일한 모집단 즉 동일한 분산을 형성하고 있다는 가정하에
위 공식이 성립하는 것이다
예를 들면,
청소년의 우울 변수에 대한 모집단이 있는데,
이 모집단에서 읍면지역의 우울로 표본 하나
중소도시 지역 우울 표본 하나,
대도시 지역 우울 표본 하나,
특별시 지역 우울 표본 하나,
이렇게 뽑아와서 평균을 비교하는 것이다
그러니, 같은 모집단에서 추출했으니
같은 분산을 보이고 있어야 한다는게 기본 가정이다
이게 그 Levene의 등분산 가정
그래서 등분산 가정이 성립하면 알던대로(?) 분산분석 실시하면 되고
만약, 그렇지 않다면 등분산 가정이 성립하지 않을 때
분산분석 해보고 싶어하신 분들이 개발한 통계방법을 쓰면 된다
뭐..Welch's F라던가
'교육통계 > 분산분석' 카테고리의 다른 글
| 분산분석 2. 분산분석 수식 해체쇼 (0) | 2023.09.04 |
|---|---|
| 분산분석 0.자 다시 시작이야~ (0) | 2023.09.04 |