앞서 통계 프로그램 다룰 때 분산분석을 기계적으로 어떻게 하는지 다루었는데,
갑자기.. 아 근데 분산분석에 대해 좀 나름 이해하고 넘어가야 좋지 않을까 싶은 생각이 들었다
석사과정일 때 맨날
교육통계 특) 아 이런 수식 그냥 넘어가도 괜찮아~
했던 게 좀 계속 걸려서
뭐 수식없이 그냥 개념만 이해해도 충분하지 않을까?
무지성으로 암기하고 넘어간다던가
했던 것들이 요새 뭔가 뭔가 마음에 걸려서
하나 하나 채워보고자ㅋㅋ
어쨌든 수식도 중요한 논리 과정인데
왜 맨날 수식 어렵니 어쩌니 이래 덮고 지나가서
계속 혼란과 혼동이 오는 것 같은 기분이라..
(나만 그런가?)
1. 일단 그래서 분산분석 왜 하는데?
두 집단 간의 평균 비교를 할 때 t-test를 했다
아 그럼 3집단 이상 있으면 어카노? 했을 때
예를 들어, 지역규모별로 청소년의 우울이 차이가 있는가?
읍면지역, 중소도시, 대도시, 특별시 총 4개 집단이 있으면.. (아 좀 많은디;;ㅋㅋ)
방법 1. 다중검정
걍 2개씩 짝지어서 검정하면 되는거 아님?
일단 영가설부터 확인해보자

평균 차이가 없다
이거에서 저거빼니 '0'이다 라는 식으로 바꿔주면,

이 모든 조건이 동시에 만족해야 한다..오마나ㅋㅋ
그냥 여기만 봐도 당장 t-test 멈춰! 해야 할 것 같지만
일단 조금만 더 알아보자
각각의 검정을 진행하면
① ~ ⑥ 까지 모두 '유의 수준'이 존재한다
통상 0.05 수준으로 α 를 잡으니까
α가 6개? 엄청 뻥튀기 된다
그럼 뭐 다 영가설 기각시키겄지ㅋㅋ
방법 2. 분산검정
분산을 활용해보자는 아이디어는 아마도 Fisher 경이 시작 같긴 한데
집단간에 분산을 비교해보자는 것은 무슨 의미가 있나 했을 때
분산이 크다라는 것은 값들이 퍼져있다
분산이 작다라는 것은 값들이 모여있다
인데 이 개념으로 어케 한다는 건가?
일단 4개 집단의 box-Plot을 그려보면

특별시와 대도시만 일단 잘라서 보면
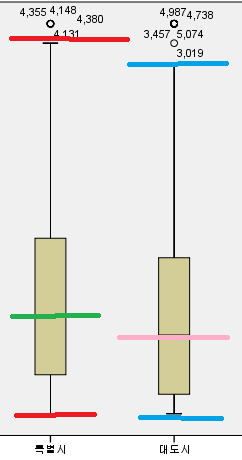
분포가 차이(빨강 vs 파랑)가 분명 존재한다
특별시 분포가 크다? 그러면 특별시 분산이 대도시에 비해 클 것이다
그리고 평균을 비교해보니,
분산이 큰 특별시의 평균(초록)이 대도시(핑크)에 비해
살짝 더 큰 것을 볼 수 있다
다음으로 옆에 중소도시, 읍면지역을 살펴보자
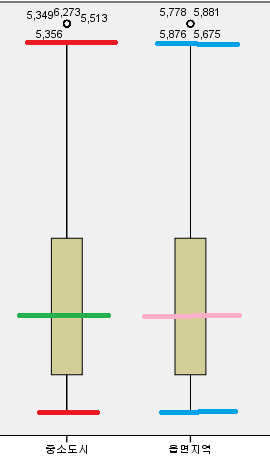
중소도시와 읍면지역의 분포는 딱히 차이가 보이지 않는다
그랬더니, 평균도 거의 유사한 것으로 보인다
실제 데이터 값으로 한 번 더 확인을 해보면
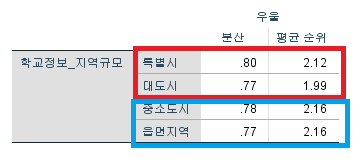
그렇게 분명한 차이는 아니지만,
분산으로 평균값을 비교할 여지가 분명 있어보인다
그럼 이제 통계적으로 어떻게 검정할 건데?
'교육통계 > 분산분석' 카테고리의 다른 글
| 분산분석 2. 분산분석 수식 해체쇼 (0) | 2023.09.04 |
|---|---|
| 분산분석 1. F분포 누구냐 넌? (0) | 2023.09.04 |